题目内容
3.已知数列{an}的前n项和为Sn,an>0,且满足:(an+2)2=4Sn+4n+1,n∈N*.(1)求a1及通项公式an;
(2)若bn=(-1)n•an,求数列{bn}的前n项和Tn.
分析 (1)利用数列递推关系、等差数列的通项公式即可得出.
(2)对n分类讨论,利用分组求和即可得出.
解答 解:(1)∵(an+2)2=4Sn+4n+1,n∈N*,∴$({a}_{1}+2)^{2}$=4a1+5,a1>0,解得a1=1.
n≥2时,$({a}_{n-1}+2)^{2}$=4Sn-1+4(n-1)+1,相减可得:${a}_{n}^{2}-$$({a}_{n-1}+2)^{2}$=0,an>0,化为:an-an-1=2.
∴数列{an}是等差数列,公差为2,首项为1.
∴an=1+2(n-1)=2n-1.
(2)bn=(-1)n•an=(-1)n•(2n-1).
n=2k(k∈N*)时,b2k-1+b2k=-(2n-1)+(2n+1)=2.
∴数列{bn}的前n项和Tn=n.
n=2k-1(k∈N*)时,b2k+b2k+1=(2n-1)-(2n+1)=-2.
∴数列{bn}的前n项和Tn=-1-$\frac{n-1}{2}×2$=-n.
∴Tn=$\left\{\begin{array}{l}{n,n=2k}\\{-n,n=2k-1}\end{array}\right.$,k∈N*.
点评 本题考查了分组求和、等差数列的通项公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.函数y=f(x)满足对任意的x,y∈R,都有f(x+y)=f(x)•f(y),且f(1)=2,若g(x)是f(x)的反函数(注:互为反函数的函数图象关于直线y=x对称),则g(8)=( )
| A. | 3 | B. | 4 | C. | 16 | D. | $\frac{1}{256}$ |
11.“a2+b2≠0”的含义为( )
| A. | a,b 不全为0 | B. | a,b全不为0 | ||
| C. | a,b 至少有一个为0 | D. | a不为0且b为0,或 b不为0且a为0 |
18.已知f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9,则函数f(x)的解析式为( )
| A. | f(x)=x+3 | B. | f(x)=x-3 | C. | f(x)=2x+3 | D. | f(x)=2x-3 |
8.已知方程$\frac{x^2}{2-k}+\frac{y^2}{2k+1}=1$表示焦点在y轴上的椭圆,则实数k的取值范围是( )
| A. | $(\frac{1}{2},2)$ | B. | (2,+∞) | C. | (1,2) | D. | $(\frac{1}{2},1)$ |
 为了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右五个小组的频率分布为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.
为了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右五个小组的频率分布为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.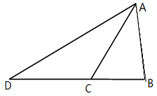 如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.
如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.