题目内容
1.以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线l的参数方程为$\left\{\begin{array}{l}{x=tsinφ}\\{y=1+tcosφ}\end{array}\right.$(t为参数,0<φ<π),曲线C的极坐标方程为ρcos2θ=4sinθ.(Ⅰ) 求直线l的普通方程和曲线C的直角坐标方程;
(II)设直线l与曲线C相交于A,B两点,当φ变化时,求|AB|的最小值.
分析 (Ⅰ) 利用三种方程的互化方法,求直线l的普通方程和曲线C的直角坐标方程;
(II)将直线l的参数方程代入x2=4y,得t2sinφ-4tcosφ-4=0,利用韦达定理,即可求|AB|的最小值.
解答 解:(Ⅰ) 由$\left\{\begin{array}{l}{x=tsinφ}\\{y=1+tcosφ}\end{array}\right.$消去t得直线l的普通方程为xcosφ-ysinφ+sinφ=0.…(2分)
由曲线ρcos2θ=4sinθ 即 ρ2cos2θ=4ρsinθ,它的直角坐标方程为 x2=4y.…(5分)
(II) 将直线l的参数方程代入x2=4y,得t2sinφ-4tcosφ-4=0,…(6分)
设A、B两点对应的参数分别为t1,t2,
则t1+t2=$\frac{4cosφ}{si{n}^{2}φ}$,t1t2=-$\frac{4}{si{n}^{2}φ}$,…(7分)
所以|AB|=|t1-t2|=$\frac{4}{si{n}^{2}φ}$.…(9分)
当φ=$\frac{π}{2}$时,|AB|的最小值为4.…(10分)
点评 本题考查三种方程的互化,考查参数方程的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
11.“a2+b2≠0”的含义为( )
| A. | a,b 不全为0 | B. | a,b全不为0 | ||
| C. | a,b 至少有一个为0 | D. | a不为0且b为0,或 b不为0且a为0 |
12.已知${({1+x})^{10}}={a_0}+{a_1}({1-x})+{a_2}{({1-x})^2}+L+{a_{10}}{({1-x})^{10}}$,则a8等于( )
| A. | -5 | B. | 5 | C. | 90 | D. | 180 |
6.已知x,y满足$\left\{\begin{array}{l}y≤x\\ x+y+2≥0\\ x≤1\end{array}\right.$,且z=y-2x的最大值是( )
| A. | 1 | B. | -1 | C. | -2 | D. | -5 |
10.下列图形中,不可能是函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
11.执行如图所示的程序框图,则输出的S的值为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
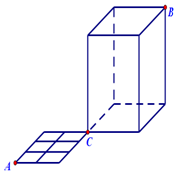 如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.
如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.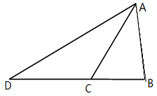 如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.
如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.