题目内容
若函数f(x)=x2+2x的图象上存在不同的两点A、B,使得曲线y=f(x)在点A、B处的切线互相垂直,则2x1-x2的最大值是 .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用,不等式的解法及应用
分析:由题意及导数的几何意义得出f′(x1)•f′(x2)=-1,化简得(x1+1)+(x2+1)=-
,然后将2x1-x2写成2(x1+1)-(x2+1)-1,再根据不等式的性质即可求解.
| 1 |
| 4 |
解答:
由导数的几何意义知,点A处切线的斜率为f′(x1),点B处的切线的斜率为f′(x2),
函数f(x)的图象在点A、B处的切线互相垂直时,
有f′(x1)•f′(x2)=-1,
即(2x1+2)(2x2+2)=-1.
从而x1+1=
.
又点A、B必在函数f(x)=x2+2x图象的对称轴x=-
=-1的两边,
显然x1<-1<x2,此时x1+1<0,x2+1>0.
故2x1-x2=2(x1+1)-(x2+1)-1
=-[-2(x1+1)+(x2+1)]-1
≤-
-1
=-
从而2x1-x2的最大值为-
.
函数f(x)的图象在点A、B处的切线互相垂直时,
有f′(x1)•f′(x2)=-1,
即(2x1+2)(2x2+2)=-1.
从而x1+1=
| -1 |
| 4(x2+1) |
又点A、B必在函数f(x)=x2+2x图象的对称轴x=-
| 2 |
| 2×1 |
显然x1<-1<x2,此时x1+1<0,x2+1>0.
故2x1-x2=2(x1+1)-(x2+1)-1
=-[-2(x1+1)+(x2+1)]-1
≤-
|
=-
| ||
| 2 |
从而2x1-x2的最大值为-
| ||
| 2 |
点评:本题主要考查导数的几何意义及不等式的性质,将2x1-x2写成2(x1+1)-(x2+1)-1,再利用(x1+1)+(x2+1)=-
是解决本题的关键.
| 1 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
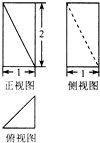
如图是某几何体的三视图,则该几何体的体积等于( )

A、
| ||
B、
| ||
| C、1 | ||
D、
|
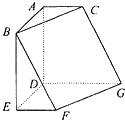 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG, 如图,已知三棱锥P-ABC中,PA⊥平面 ABC,△ABC是正三角形,AC=2 PA=2,D、E分别为棱 AC和 BC的中点.
如图,已知三棱锥P-ABC中,PA⊥平面 ABC,△ABC是正三角形,AC=2 PA=2,D、E分别为棱 AC和 BC的中点.