题目内容
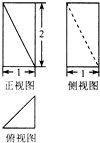
如图是某几何体的三视图,则该几何体的体积等于( )

A、
| ||
B、
| ||
| C、1 | ||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是三棱柱削去一个同高的三棱锥,根据三视图判断相关几何量的数据,把数据代入棱柱与棱锥的体积公式计算.
解答:
解:由三视图知:几何体是三棱柱削去一个同高的三棱锥,
其中三棱柱的高为2,底面是直角边长为1的等腰直角三角形,
三棱锥的底面是直角边长为1的等腰直角三角形,
∴几何体的体积V=
×1×1×2-
×
×1×1×2=
.
故选:A.
其中三棱柱的高为2,底面是直角边长为1的等腰直角三角形,
三棱锥的底面是直角边长为1的等腰直角三角形,
∴几何体的体积V=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
故选:A.
点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
若平面向量
,
满足|
+
|=1,且
=2
,则|
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
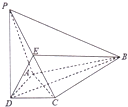 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2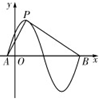 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,把∠APB=θ,则tanθ的值是( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,把∠APB=θ,则tanθ的值是( )