题目内容
已知函数f(x)的自变量取值区间为A,若其值域也为A,则称区间A为f(x)的保值区间.若函数g(x)=x+m-lnx的保值区间是[
,+∞),则m的值为 .
| 1 |
| 2 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:由题意可得g(x)=x+m-lnx在x∈[
,+∞)的值域为[
,+∞),求导数可得g(x)的单调性,可得g(1)=
,解m的方程可得.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由题意可得g(x)=x+m-lnx在x∈[
,+∞)的值域为[
,+∞),
求导数可得g′(x)=1-
=
,
令g′(x)=
<0,可解得0<x<1,
∴g(x)=x+m-lnx在x∈[
,1)单调递减,
同理由g′(x)>0,可解得x>1,
∴g(x)=x+m-lnx在x∈(1,+∞)单调递增,
∴当x=1时,函数g(x)=x+m-lnx取最小值,
∴g(1)=1+m-ln1=
,解得m=-
故答案为:-
.
| 1 |
| 2 |
| 1 |
| 2 |
求导数可得g′(x)=1-
| 1 |
| x |
| x-1 |
| x |
令g′(x)=
| x-1 |
| x |
∴g(x)=x+m-lnx在x∈[
| 1 |
| 2 |
同理由g′(x)>0,可解得x>1,
∴g(x)=x+m-lnx在x∈(1,+∞)单调递增,
∴当x=1时,函数g(x)=x+m-lnx取最小值,
∴g(1)=1+m-ln1=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查对数函数的性质,涉及导数法判函数的单调性,属中档题.

练习册系列答案
相关题目
已知
,
是两个单位向量,下列命题中错误的是( )
| a |
| b |
A、|
| ||||||||||
B、
| ||||||||||
C、当
| ||||||||||
D、当
|
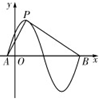 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,把∠APB=θ,则tanθ的值是( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,把∠APB=θ,则tanθ的值是( )