题目内容
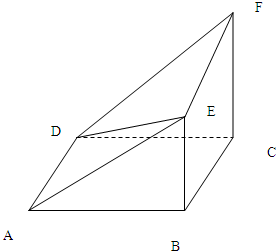 多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.
多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.(Ⅰ)求证:DE⊥AC;
(Ⅱ)求平面EFD与平面ABCD所成的锐二面角.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:证明题
分析:(Ⅰ)根据BE⊥平面ABCD,可知BD为DE为在底面ABCD上的射影,在正方形ABCD中,AC⊥BD,故可利用三垂线定理即得结论;
(Ⅱ)先作出二面角F-DG-C的平面角,延长FE与CB,交于点G,连接DG,则DG为平面EFD与平面ABCD的交线,过C作CH⊥DG交DG于H,连接FH,则∠FHC为二面角F-DG-C的平面角,从而可求锐二面角.
(Ⅱ)先作出二面角F-DG-C的平面角,延长FE与CB,交于点G,连接DG,则DG为平面EFD与平面ABCD的交线,过C作CH⊥DG交DG于H,连接FH,则∠FHC为二面角F-DG-C的平面角,从而可求锐二面角.
解答:
 (Ⅰ)证明:连接BD
(Ⅰ)证明:连接BD
∵BE⊥平面ABCD
∴BD为DE为在底面ABCD上的射影
∴在正方形ABCD中,AC⊥BD…
∴DE⊥AC…4分
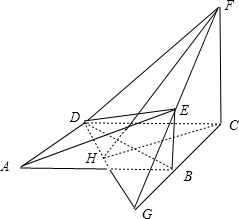
(Ⅱ)解:延长FE与CB,交于点G,连接DG,则DG为平面EFD与平面ABCD的交线,
过C作CH⊥DG交DG于H,连接FH
∵FC⊥平面ABCD,
∴CH为FH在面ABCD上的射影
∴FH⊥DG
∴∠FHC为二面角F-DG-C的平面角 8分
设BE=1,在△DCG中,CH=
=
在△FCH中,FC=2,
∴tan∠FHC=
=
∴所求锐二面角为arctan
…12分
 (Ⅰ)证明:连接BD
(Ⅰ)证明:连接BD∵BE⊥平面ABCD
∴BD为DE为在底面ABCD上的射影
∴在正方形ABCD中,AC⊥BD…
∴DE⊥AC…4分
(Ⅱ)解:延长FE与CB,交于点G,连接DG,则DG为平面EFD与平面ABCD的交线,
过C作CH⊥DG交DG于H,连接FH
∵FC⊥平面ABCD,
∴CH为FH在面ABCD上的射影
∴FH⊥DG
∴∠FHC为二面角F-DG-C的平面角 8分
设BE=1,在△DCG中,CH=
| 2×4 | ||
|
| 4 | ||
|
在△FCH中,FC=2,
∴tan∠FHC=
2
| ||
| 4 |
| ||
| 2 |
∴所求锐二面角为arctan
| ||
| 2 |
点评:本题以多面体为载体,考查线面垂直,考查三垂线定理,考查面面角,解题的关键是正确运用三垂线定理,作出面面角.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
直角坐标平面内,过点P(2,1)且与圆x2+y2=4相切的直线( )
| A、有两条 | B、有且仅有一条 |
| C、不存在 | D、不能确定 |
已知直线z的极坐标方程为ρcos(θ-
) =
,点A的极坐标为(4,
),则点A到直线l的距离为( )
| 3π |
| 4 |
| 2 |
| π |
| 4 |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |