题目内容
已知α为锐角,且tanα=
-1.
(1)设
=(x,1),
=(2tan2α,sin(2α+
)),若
⊥
,求x的值;
(2)在△ABC中,若∠A=2α,∠C=
,BC=2,求△ABC的面积.
| 2 |
(1)设
| m |
| n |
| π |
| 4 |
| m |
| n |
(2)在△ABC中,若∠A=2α,∠C=
| π |
| 3 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:计算题
分析:(1)利用二倍角的正切公式求得tan2α 的值,可得2α=
,再由
•
=0求得x的值.
(2)由(1)得∠A=
,而∠C=
,根据正弦定理求得AB的值,可得sinB的值,从而求得△ABC的面积.
| π |
| 4 |
| m |
| n |
(2)由(1)得∠A=
| π |
| 4 |
| π |
| 3 |
解答:
解:(1)∵tanα=
-1,tan2α=
=
=1.…(2分)
又∵α为锐角,∴2α=
,α=
,
=(2,1).…(4分)
∵
⊥
,∴
•
=0,即 2x+1=0,x=-
. …(6分)
(2)由(1)得∠A=
,而∠C=
,根据正弦定理得
=
,…(8分)
求得AB=
,…(10分)
∴sinB=sin(A+C)=
,…(12分)
从而求得△ABC的面积S=
AB•BC•sinB=
.…(14分)
| 2 |
| 2tanα |
| 1-tan2α |
2(
| ||
1- (
|
又∵α为锐角,∴2α=
| π |
| 4 |
| π |
| 8 |
| n |
∵
| m |
| n |
| m |
| n |
| 1 |
| 2 |
(2)由(1)得∠A=
| π |
| 4 |
| π |
| 3 |
| AB | ||
sin
|
| 2 | ||
sin
|
求得AB=
| 6 |
∴sinB=sin(A+C)=
| ||||
| 4 |
从而求得△ABC的面积S=
| 1 |
| 2 |
3+
| ||
| 2 |
点评:本题主要考查三角函数的恒等变换,向量的数量积公式的应用,两个向量垂直的性质,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
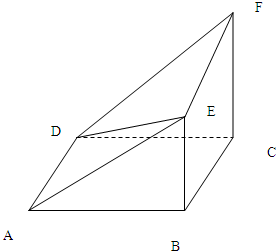 多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.
多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.