题目内容
若随机变量ξ服从几何分布,且p(ξ=k)=g(k,p)(0<p<1),试写出随机变量ξ的期望公式,并给出证明.
考点:离散型随机变量的期望与方差,超几何分布的应用
专题:计算题,证明题
分析:根据变量符合几何分布,写出各个变量对应的概率,表示出期望的表达式,利用数列中的错位相减得到数列的前n项和,根据n是一个趋近于无穷的数字,利用极限的思想得到结果.
解答:
证明:如下表
ξ 1 2 3 4 …k …
P p qp q2p q3p …qk-1p …
则Eξ=p+2qp+3q2p+…+kqk-1p+…
=p(1+2q+3q2+…+kqk-1+…)
令T=1+2q+3q2+4q3 …+kqk-1+(k+1)qk +…①
则qT=q+2q2+3q3+…+(k-1)qk-1+kqk+…②
①-②T-qT=q0+q1+q2+q3+…+qk-1+qk +…
=
即T=
=
,
则Eξ=
,
∴当n→∞时,Eξ=
ξ 1 2 3 4 …k …
P p qp q2p q3p …qk-1p …
则Eξ=p+2qp+3q2p+…+kqk-1p+…
=p(1+2q+3q2+…+kqk-1+…)
令T=1+2q+3q2+4q3 …+kqk-1+(k+1)qk +…①
则qT=q+2q2+3q3+…+(k-1)qk-1+kqk+…②
①-②T-qT=q0+q1+q2+q3+…+qk-1+qk +…
=
| 1(1-qn) |
| 1-q |
即T=
| 1-qn |
| (1-q)2 |
| 1-qn |
| p2 |
则Eξ=
| 1-qn |
| p |
∴当n→∞时,Eξ=
| 1 |
| p |
点评:本题看出几何分布的期望值的推导,本题解题的关键是利用数列的求和的方法来写出期望的表示式,本题是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
(
)n存在,则实数a的取值范围是( )
| lim |
| n→∞ |
| 1-a |
| a |
A、(-
| ||||
B、[
| ||||
| C、(-∞,1) | ||||
D、(
|
盒子里有25个外形相同的球,其中10个白的,5个黄的,10个黑的,从盒子中任意取出一球,已知它不是白球,则它是黑球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=
的定义域是A,B={x|(
)x<1},则A∩B=( )
| -x2+x+6 |
| 5 |
| 3 |
| A、{x|x≤-2} |
| B、{x|-3≤x<0} |
| C、{x|0<x≤3} |
| D、{x|-2≤x<0} |
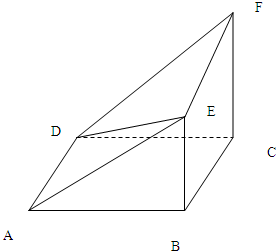 多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.
多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE. 如图所示,向正方形任意抛掷一点,此点不落在阴影部分的概率是
如图所示,向正方形任意抛掷一点,此点不落在阴影部分的概率是