题目内容
已知直线z的极坐标方程为ρcos(θ-
) =
,点A的极坐标为(4,
),则点A到直线l的距离为( )
| 3π |
| 4 |
| 2 |
| π |
| 4 |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |
考点:简单曲线的极坐标方程,点到直线的距离公式
专题:计算题
分析:利用两角差的余弦函数展开方程,把极坐标方程化为普通方程,求出A的直角坐标,利用点到直线的距离公式求解即可.
解答:
解:因为ρcos(θ-
) =
可化为:-
ρ cosθ+
ρsinθ=
,
直线z的直角坐标方程为:x-y+2=0,
点A的极坐标为(4,
),它的直角坐标(2
,2
),
则A到直线的距离为:d=
=
.
故选C.
| 3π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
直线z的直角坐标方程为:x-y+2=0,
点A的极坐标为(4,
| π |
| 4 |
| 2 |
| 2 |
则A到直线的距离为:d=
|2
| ||||
|
| 2 |
故选C.
点评:本题是基础题,考查极坐标与直角坐标的互化,点到直线的距离公式的应用,考查计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
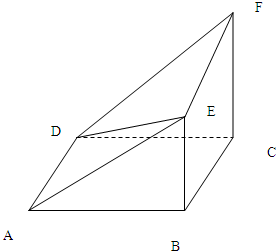 多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.
多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.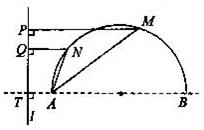 如图,已知半圆的直径|AB|=20,l为半圆外一直线,且与BA的延长线交于点T,|AT|=4,半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件
如图,已知半圆的直径|AB|=20,l为半圆外一直线,且与BA的延长线交于点T,|AT|=4,半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,