题目内容
(理)数列{an}中,a1=
,an+1=sin(
+an),n∈N*.
求证:(1)0<an<1;
(2)an<an+1;
(3)1-an<
(1-an-1).(n≥2)
(参考公式:sinα+sinβ=2sin
cos
)
| 1 |
| 2 |
| π |
| 2 |
求证:(1)0<an<1;
(2)an<an+1;
(3)1-an<
| π |
| 4 |
(参考公式:sinα+sinβ=2sin
| α+β |
| 2 |
| α-β |
| 2 |
考点:数列与不等式的综合,数列递推式
专题:证明题
分析:(1)、(2)前两小问可一起进行证明.先看当n=1时,可求得a2,则可验证结论成立;假设n=k时结论成立,根据0<ak<ak+1<1,推断出0<
ak<
ak+1<
.进而可知0<sin(
ak)<sin(
ak+1)<1,即0<ak+1<ak+2<1,结论成立,最后综合可知(1)(2)成立.
(3)由于1<1+a n-1<2,结合(1)(2)中的结论得出
(1+a1)的取值范围,从而1-a n=sin
-sin(
a n-1)=2cos[
(1+a n-1)]sin[
(1-a n-1)]<sin[
(1-a n-1)],根据0<[
(1-a n-1)]<
,结合三角函数的性质sinθ<θ即可证得结论.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(3)由于1<1+a n-1<2,结合(1)(2)中的结论得出
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
解答:
证明:(1)(2)①n=1时,a1=
,
由于条件an+1=sin(
•an),
∴a2=sin(
a1)=sin
=
.
∴0<a1<a2<1,故结论成立.
②假设n=k时结论成立,
即0<ak<ak+1<1,
则0<
ak<
ak+1<
.
∴0<sin(
ak)<sin(
ak+1)<1,
即0<ak+1<ak+2<1,
也就是说n=k+1时,结论也成立.
由①②可知,对一切n∈N*均有0<an<an+1<1.
(3)∵1<1+a n-1<2,
∴
<
(1+a n-1)<
,
又an<an+1,
∴1+a n-1≥1+a1,(n≥2)
∴
(1+a n-1)≥
(1+a1)=
>
,
∴1-a n=sin
-sin(
a n-1)=2cos[
(1+a n-1)]sin[
(1-a n-1)]<sin[
(1-a n-1)]
∵0<[
(1-a n-1)]<
,又θ是锐角时,sinθ<θ,
∴sin[
(1-a n-1)]<
(1-a n-1)
∴1-an<
(1-an-1).(n≥2).
| 1 |
| 2 |
由于条件an+1=sin(
| π |
| 2 |
∴a2=sin(
| π |
| 2 |
| π |
| 4 |
| ||
| 2 |
∴0<a1<a2<1,故结论成立.
②假设n=k时结论成立,
即0<ak<ak+1<1,
则0<
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴0<sin(
| π |
| 2 |
| π |
| 2 |
即0<ak+1<ak+2<1,
也就是说n=k+1时,结论也成立.
由①②可知,对一切n∈N*均有0<an<an+1<1.
(3)∵1<1+a n-1<2,
∴
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
又an<an+1,
∴1+a n-1≥1+a1,(n≥2)
∴
| π |
| 4 |
| π |
| 4 |
| 3π |
| 8 |
| π |
| 3 |
∴1-a n=sin
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∵0<[
| π |
| 4 |
| π |
| 2 |
∴sin[
| π |
| 4 |
| π |
| 4 |
∴1-an<
| π |
| 4 |
点评:本题主要考查了数列递推式、数列与不等式的综合、不等式证明等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知点P1(0,0),P2(1,1),P3(0,
),则在3x+2y-1≤0表示的平面区域内的点是( )
| 1 |
| 3 |
| A、P1,P2 |
| B、P1,P3 |
| C、P2,P3 |
| D、P2 |
盒子里有25个外形相同的球,其中10个白的,5个黄的,10个黑的,从盒子中任意取出一球,已知它不是白球,则它是黑球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
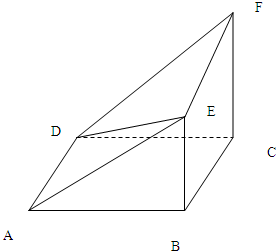 多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.
多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE. 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,