题目内容
直角坐标平面内，过点P（2，1）且与圆x2+y2=4相切的直线（ ）
| A、有两条 | B、有且仅有一条 |
| C、不存在 | D、不能确定 |
考点：直线与圆的位置关系
专题：计算题
分析：由圆的方程找出圆心坐标和半径r．利用两点间的距离公式求出P到圆心间的距离d，用d与r比较大小，可得出P在圆外，则过P与圆相切的直线有两条．
解答：
解：由圆x2+y2=4，得到圆心坐标为（0，0），半径r=2，
∵P到圆心的距离d=
=
＞2=r，
∴点P在圆外，
则过点P且与圆相切的直线有两条．
故选A
∵P到圆心的距离d=
| (2-0)2+(1-0)2 |
| 5 |
∴点P在圆外，
则过点P且与圆相切的直线有两条．
故选A
点评：此题考查了点与圆的位置关系，以及圆的切线方程，当点在圆内时，过此点不能作圆的切线；当点在圆上时，过此点作圆的切线，此时切线只有一条；当点在圆外时，过此点作圆的切线，此时切线有两条．故判断出点P与圆的位置关系是解本题的关键．
练习册系列答案
相关题目
已知点P1(0，0)，P2(1，1)，P3(0，
)，则在3x+2y-1≤0表示的平面区域内的点是（ ）
| 1 |
| 3 |
| A、P1，P2 |
| B、P1，P3 |
| C、P2，P3 |
| D、P2 |
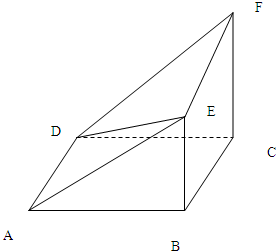多面体EF-ABCD中，ABCD为正方形，BE⊥平面ABCD，CF⊥平面ABCD，AB=CF=2BE．
已知E，F，G，H分别是空间四边形四条边AB，BC，CD，DA的中点，