题目内容
函数f(x)=x(
+
)定义域为(-∞,1)∪(1,+∞),则满足不等式ax≥f(a)的实数x的集合为 .
| 1 |
| 2x-a |
| 1 |
| 2 |
考点:指数函数综合题
专题:计算题
分析:由题意可得a=2,f(x)=x(
+
),f(a)=f(2)=2,由ax≥f(a),结合指数函数单调性可求x
| 1 |
| 2x-2 |
| 1 |
| 2 |
解答:
解:由函数f(x)=x(
+
)定义域为(-∞,1)∪(1,+∞),可知a=2
∴f(x)=x(
+
),f(a)=f(2)=2
由ax≥f(a)可得,2x≥2
∴x≥1
故答案为{x|x≥1}
| 1 |
| 2x-a |
| 1 |
| 2 |
∴f(x)=x(
| 1 |
| 2x-2 |
| 1 |
| 2 |
由ax≥f(a)可得,2x≥2
∴x≥1
故答案为{x|x≥1}
点评:本题主要考查了函数的定义域的应用,指数函数的单调性的应用,属于基础试题

练习册系列答案
相关题目
已知点P1(0,0),P2(1,1),P3(0,
),则在3x+2y-1≤0表示的平面区域内的点是( )
| 1 |
| 3 |
| A、P1,P2 |
| B、P1,P3 |
| C、P2,P3 |
| D、P2 |
若
(
)n存在,则实数a的取值范围是( )
| lim |
| n→∞ |
| 1-a |
| a |
A、(-
| ||||
B、[
| ||||
| C、(-∞,1) | ||||
D、(
|
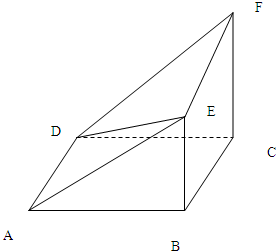 多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.
多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.