题目内容
已知函数f(x)=x+sinx,项数为19的等差数列{an}的公差d≠0,若f(a1)+f(a2)+…+f(a18)+f(a19)=0,则当k= 时,f(ak)=0.
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:利用奇函数与等差数列的性质即可得出.
解答:
解:由函数f(x)=x+sinx,可得f(-x)=-f(x),因此函数f(x)是奇函数,其图象关于原点对称.
∵项数为19的等差数列{an}的公差d≠0,且f(a1)+f(a2)+…+f(a18)+f(a19)=0,
∴等差数列{an}的19项在一条直线上且关于原点对称,
∴f(a1)+f(a19)=f(a2)+f(a18)=…=2f(a10)=0,
因此当k=10时,f(a10)=0.
故答案为:10.
∵项数为19的等差数列{an}的公差d≠0,且f(a1)+f(a2)+…+f(a18)+f(a19)=0,
∴等差数列{an}的19项在一条直线上且关于原点对称,
∴f(a1)+f(a19)=f(a2)+f(a18)=…=2f(a10)=0,
因此当k=10时,f(a10)=0.
故答案为:10.
点评:本题考查了奇函数与等差数列的性质,考查了推理能力,属于基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
设函数f(x)满足f(x+π)=f(x)+cosx,当0≤x≤π时,f(x)=0,则f(
)=( )
| 11π |
| 3 |
A、
| ||||
B、
| ||||
| C、0 | ||||
D、-
|
已知点P是双曲线
-y2=1上任意一点,过点P分别作双曲线的两条渐近线的垂线,垂足分别为A、B,则
•
=( )
| x2 |
| 4 |
| PA |
| PB |
A、-
| ||
B、
| ||
C、-
| ||
D、-
|
已知m,n为异面直线,m?平面α,n?平面β,α∩β=l,则直线l( )
| A、与m,n 都相交 |
| B、至多与m,n 中的一条相交 |
| C、与m,n 都不相交 |
| D、与m,n 至少一条相交 |
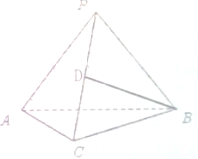 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,且PA=PC=2.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,且PA=PC=2.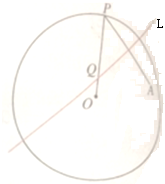 如图,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点,线段AP的垂直平分线L和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?
如图,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点,线段AP的垂直平分线L和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?