题目内容
对具有线性相关关系的变量x,y有一组观测数据(xi,yi)(i=1,2,…6),若x1+x2+…+x6=2(y1+y2+…+y6)=6,其回归直线方程是
=
x+a,则实数a的值是( )
 |
| y |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:线性回归方程
专题:计算题,概率与统计
分析:求出横标和纵标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程即可.
解答:
解:∵x1+x2+…+x6=2(y1+y2+…+y6)=6,
∴
=1,
=
,
∴这组数据的样本中心点是(1,
),
把样本中心点代入回归直线方程
=
x+a得:
=
+a,
解得a=
,
故选B.
∴
. |
| x |
. |
| y |
| 1 |
| 2 |
∴这组数据的样本中心点是(1,
| 1 |
| 2 |
把样本中心点代入回归直线方程
 |
| y |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解得a=
| 1 |
| 6 |
故选B.
点评:本题考查线性回归方程,解题的关键是线性回归直线一定过样本中心点,这是求解线性回归方程的步骤之一.属于基础题.

练习册系列答案
相关题目
已知m,n为异面直线,m?平面α,n?平面β,α∩β=l,则直线l( )
| A、与m,n 都相交 |
| B、至多与m,n 中的一条相交 |
| C、与m,n 都不相交 |
| D、与m,n 至少一条相交 |
下列函数中,其图象既是轴对称图形又在区间(0,+∞)上单调递增的是( )
A、y=
| ||
| B、y=-x2+1 | ||
| C、.y=2x | ||
| D、y=lg|x+1| |
函数y=
的对称中心是( )
| x+3 |
| x-2 |
| A、(2,3) |
| B、(2,1) |
| C、(-2,1) |
| D、(-2,3) |
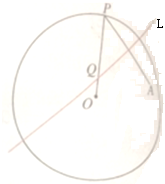 如图,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点,线段AP的垂直平分线L和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?
如图,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点,线段AP的垂直平分线L和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么? 一个正方体挖去一个圆锥得到一个几何体,其正视图与俯视图如图所示,则该几何体的侧(左)视图是( )
一个正方体挖去一个圆锥得到一个几何体,其正视图与俯视图如图所示,则该几何体的侧(左)视图是( )


