题目内容
在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,PD=AB=2,则此四棱锥的内切球与外接球的半径分别为( )
A、2-
| ||||||||
B、
| ||||||||
C、,2-
| ||||||||
D、
|
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:四棱锥的外接球,为棱长为2的正方体的外接球,直径为2
,半径为
,利用等体积计算四棱锥的内切球半径.
| 3 |
| 3 |
解答:
解:四棱锥的外接球,为棱长为2的正方体的外接球,直径为2
,半径为
,
设四棱锥的内切球半径为r,则
×2×2×2=
×(2×2+2×
×2×2+2×
×2×2
)r,
∴r=2-
,
故选:A.
| 3 |
| 3 |
设四棱锥的内切球半径为r,则
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴r=2-
| 2 |
故选:A.
点评:本题考查四棱锥的内切球与外接球的半径,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知双曲线
-
=1的一个焦点在圆x2+y2-4x-5=0上,则双曲线的渐近线方程为( )
| x2 |
| 9 |
| y2 |
| m |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
已知m,n为异面直线,m?平面α,n?平面β,α∩β=l,则直线l( )
| A、与m,n 都相交 |
| B、至多与m,n 中的一条相交 |
| C、与m,n 都不相交 |
| D、与m,n 至少一条相交 |
 如图RT△O′A′B′是一个平面图形的直观图,若O′B′=
如图RT△O′A′B′是一个平面图形的直观图,若O′B′=| 2 |
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|
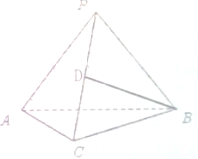 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,且PA=PC=2.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,且PA=PC=2.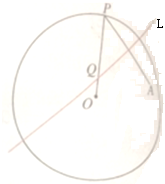 如图,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点,线段AP的垂直平分线L和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?
如图,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点,线段AP的垂直平分线L和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?