题目内容
记函数f(x)=lg(x2-x-2)的定义域为集合A,函数g(x)=
的定义域为集合B.
(1)求A∩B;
(2)若C={x|(x+2-p)(x+2+p)<0,p>0},且C⊆(A∩B)求实数p的取值范围.
| 3-|x| |
(1)求A∩B;
(2)若C={x|(x+2-p)(x+2+p)<0,p>0},且C⊆(A∩B)求实数p的取值范围.
考点:集合的包含关系判断及应用,交集及其运算
专题:计算题,集合
分析:(1)求解x2-x-2>0,3-|x|≥0,从而求出A∩B;
(2)化简集合C,由C⊆(A∩B)可得不等式组,从而解出实数p的取值范围.
(2)化简集合C,由C⊆(A∩B)可得不等式组,从而解出实数p的取值范围.
解答:
解:(1)由题意,x2-x-2>0,
解得,x>2或x<-1,
3-|x|≥0,
解得,-3≤x≤3,
则A∩B={x|-3≤x<-1或2<x≤3}.
(2)∵p>0,
∴C={x|(x+2-p)(x+2+p)<0}=(2-p,2+p),
∵C⊆(A∩B),
∴
,
解得,0≤p≤1.
解得,x>2或x<-1,
3-|x|≥0,
解得,-3≤x≤3,
则A∩B={x|-3≤x<-1或2<x≤3}.
(2)∵p>0,
∴C={x|(x+2-p)(x+2+p)<0}=(2-p,2+p),
∵C⊆(A∩B),
∴
|
解得,0≤p≤1.
点评:本题考查了集合的化简与集合的运算,同时考查了函数的定义域的求法及集合的相互关系,属于中档题.

练习册系列答案
相关题目
已知不等式
>1的解集为(-2,a),则实数a的值为( )
| ax |
| x+2 |
| A、-2 | B、-1 | C、1 | D、2 |
用二分法求函数f(x)=x3+x2-2x-2的一个零点,依次计算得到如表函数值:
那么方程x3+x2-2x-2=0的一个近似根在下列哪两数之间( )
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
| A、1.25~1.375 |
| B、1.375~1.4065 |
| C、1.4065~1.438 |
| D、1.438~1.5 |
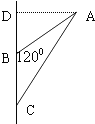 在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是( )
在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a2-c2+b2=-
ab,则角C=( )
| 3 |
| A、150° | B、60° |
| C、30° | D、45°或135° |