题目内容
19．已知函数f（x）=x2-2ax+a（a为实常数）．设$h（x）=\frac{f（x）}{x}$，证明：当a＜1时，h（x）在[1，+∞）上单调递增．分析 求出函数h（x）的表达式和导数，利用函数单调性和导数的关系进行证明即可．
解答 证明：∵f（x）=x2-2ax+a，
∴$h（x）=\frac{f（x）}{x}$=$\frac{{x}^{2}-2ax+a}{x}$=x+$\frac{a}{x}$-2a，
函数的导数h′（x）=1-$\frac{a}{{x}^{2}}$=$\frac{{x}^{2}-a}{{x}^{2}}$，
当a＜1时，x≥1得h′（x）＞0，即函数h（x）在[1，+∞）上单调递增．
点评 本题主要考查函数单调性的判断和证明，利用导数法是解决本题的关键．
练习册系列答案
相关题目
11．
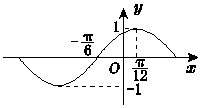已知函数f（x）=Asin（ωx+φ）（A、ω＞0）的图象如图所示，则其解析式可以是（ ）
已知函数f（x）=Asin（ωx+φ）（A、ω＞0）的图象如图所示，则其解析式可以是（ ）| A． | $y=sin（{x+\frac{π}{6}}）$ | B． | $y=sin（{x+\frac{π}{3}}）$ | C． | $y=sin（{2x-\frac{2π}{3}}）$ | D． | $y=sin（{2x+\frac{π}{3}}）$ |