题目内容

14．已知函数$f（x）=\sqrt{{x^2}+mx+1}$的定义域为R，则实数m的取值范围是[-2，2]．

分析 根据函数的定义域为R，转化为不等式恒成立进行求解即可．

解答 解：函数$f（x）=\sqrt{{x^2}+mx+1}$的定义域为R，
则等价为x2+mx+1≥0恒成立，
即判别式△=m2-4≤0，即-2≤m≤2，
故答案为：[-2，2]

点评 本题主要考查函数定义域的应用，根据根式的性质转化为不等式恒成立是解决本题的关键．

练习册系列答案
相关题目
4．设函数f（x）=4x，g（x）=$\frac{{\sqrt{x+1}}}{x}$，则f（x）•g（x）=4$\sqrt{x+1}$，（x≥-1且x≠0）．
5．方程lg（x2-3）=lg（3x-5）的解是2．
2．若f（x）=|log2x|-m有两个零点x1，x2（x1＞x2），则${x_1}^2+4{x_2}^2$的最小值为4．
9．f（x）=2x-1，且$f（m）=\frac{1}{8}$，则m=-2．
19．已知函数f（x）=x2-2ax+a（a为实常数）．设$h（x）=\frac{f（x）}{x}$，证明：当a＜1时，h（x）在[1，+∞）上单调递增．
6．设[x]表示不超过x的最大整数，用数组$[{\frac{1^2}{100}}]\;，\;\;[{\frac{2^2}{100}}]\;，\;\;[{\frac{3^2}{100}}]\;，\;…\;\;，\;[{\frac{{{{100}^2}}}{100}}]$组成集合A的元素的个数是76．
3．已知实数x，y满足2x+y+10=0，那么$\sqrt{{x^2}+{y^2}}$的最小值为（　　）
A．$\sqrt{5}$B．$\sqrt{10}$C．$2\sqrt{5}$D．$2\sqrt{10}$
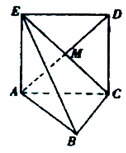4．如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC
（1）求直线AB与平面EBC所成的角的大小；
（2）求二面角A-EB-C的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网