题目内容
10.函数$y=\sqrt{1-2x}$的反函数的值域是$(-∞,\frac{1}{2}]$.分析 反函数的值域是原函数的定义域,即可得出.
解答 解:由函数$y=\sqrt{1-2x}$,可得1-2x≥0,解得x$≤\frac{1}{2}$,可得原函数的定义域:$(-∞,\frac{1}{2}]$.
则反函数的值域是$y=\sqrt{1-2x}$的定义域$(-∞,\frac{1}{2}]$.
故答案为:$(-∞,\frac{1}{2}]$.
点评 本题考查了函数的定义域、不等式的解法、互为反函数的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
20.一扇形的圆心角为60°,所在圆的半径为6,则它的面积是( )
| A. | 6π | B. | 3π | C. | 12π | D. | 9π |
20.己知函数f(x)=x3-3x,若过点A(1,m)可作曲线y=f(x)的三条切线,则实数m的取值范围是( )
| A. | -1<m<1 | B. | -4<m<4 | C. | -1<m<-2 | D. | -3<m<-2 |
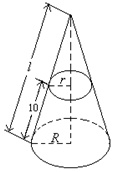 把一个圆锥截成圆台,已知圆台的上、下底面半径分别为1cm、4cm,母线长10cm.
把一个圆锥截成圆台,已知圆台的上、下底面半径分别为1cm、4cm,母线长10cm.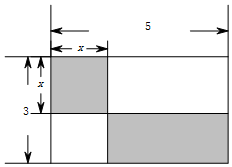 如图,一个长为5、宽为3的矩形被平行于边的两条直线所分割,其中矩形的左上角是一个是一个边长为x的正方形
如图,一个长为5、宽为3的矩形被平行于边的两条直线所分割,其中矩形的左上角是一个是一个边长为x的正方形