题目内容
对实数a和b,定义运算“?”:a?b=
,设函数f(x)=(x2-2)?(x-1),x∈R,
(1)求函数f(x)的单调区间;
(2)若函数f(x)=c恰有两个实根,求实数c的取值范围.
|
(1)求函数f(x)的单调区间;
(2)若函数f(x)=c恰有两个实根,求实数c的取值范围.
考点:函数的零点与方程根的关系,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)由新定义写出分段函数,然后画出图象,数形结合得到单调期间;
(2)直接由函数图象得到使函数f(x)=c恰有两个实根的实数c的取值范围.
(2)直接由函数图象得到使函数f(x)=c恰有两个实根的实数c的取值范围.
解答:
解:(1)由a?b=
,得f(x)=(x2-2)?(x-1)=
,
其图象如图,
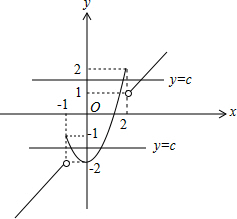
由图可知,函数的增区间为:(-∞,-1),[0,2],(2,+∞);函数的减区间为[-1,2].
(2)由图可知,使函数f(x)=c恰有两个实根的实数c的取值范围是(-2,-1]∪(1,2].
|
|
其图象如图,
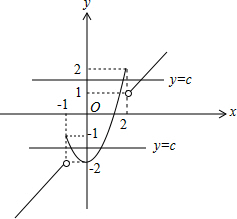
由图可知,函数的增区间为:(-∞,-1),[0,2],(2,+∞);函数的减区间为[-1,2].
(2)由图可知,使函数f(x)=c恰有两个实根的实数c的取值范围是(-2,-1]∪(1,2].
点评:本题是新定义题,考查了分段函数的应用,考查了函数零点的判断方法及数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
设a=
,b=sin85°-
cos85°,c=2(sin47°sin66°-sin24°sin43°)则a、b、c的大小关系是( )
| 4tan12.5° |
| 1-tan212.5° |
| 3 |
| A、b>c>a |
| B、a>b>c |
| C、b>a>c |
| D、c>b>a |