题目内容
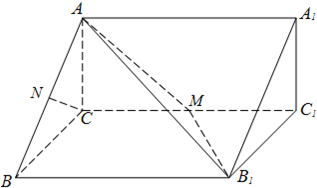 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.(1)求证:BC⊥AM;
(2)若N是AB的中点,且CN∥平面AB1M,求CM的长.
考点:直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)由线面垂直得BC⊥C1C,又BC⊥AC,从而BC⊥平面ACC1A1,由此能证明BC⊥AM.
(2)取AB1的中点P,连接MP,NP,由三角形中位线定理得NP∥BB1,从而得到PNCM是平行四边形,由此能求出CM的长.
(2)取AB1的中点P,连接MP,NP,由三角形中位线定理得NP∥BB1,从而得到PNCM是平行四边形,由此能求出CM的长.
解答:
(1)证明:∵ABC-A1B1C1为直三棱柱,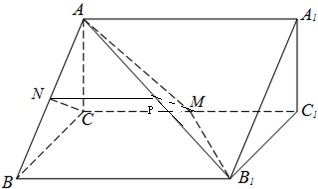
∴C1C⊥平面ABC,∴BC⊥C1C,
又BC⊥AC,∴BC⊥平面ACC1A1,
∵AM在平面ACC1A1上,∴BC⊥AM.
(2)解:取AB1的中点P,连接MP,NP,
∵P为AB1中点,N为AB中点,
∴NP为△ABB1的中位线,∴NP∥BB1,
又∵C1C,B1B都是直三棱柱的棱,∴C1C∥B1B,∴MC∥B1B,
∴NP∥CM,∴NPCM共面,
又∵CN∥平面AB1M,∴CN
MP,∴PNCM是平行四边形,
∴CM=NP=
BB1=
CC1=
×4=2.

∴C1C⊥平面ABC,∴BC⊥C1C,
又BC⊥AC,∴BC⊥平面ACC1A1,
∵AM在平面ACC1A1上,∴BC⊥AM.
(2)解:取AB1的中点P,连接MP,NP,
∵P为AB1中点,N为AB中点,
∴NP为△ABB1的中位线,∴NP∥BB1,
又∵C1C,B1B都是直三棱柱的棱,∴C1C∥B1B,∴MC∥B1B,
∴NP∥CM,∴NPCM共面,
又∵CN∥平面AB1M,∴CN
| ∥ |
. |
∴CM=NP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本小题线线平行、直线与平面的平行、线面所成角、探索性问题等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
设a=
,b=sin85°-
cos85°,c=2(sin47°sin66°-sin24°sin43°)则a、b、c的大小关系是( )
| 4tan12.5° |
| 1-tan212.5° |
| 3 |
| A、b>c>a |
| B、a>b>c |
| C、b>a>c |
| D、c>b>a |
抛掷两枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 方程
方程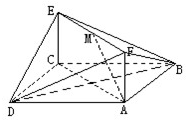 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=