题目内容
已知函数f（x）=x3+f′（1）x2-x，则函数f（x）的图象在点（1，f（1））处的切线方程是 ．
考点：利用导数研究曲线上某点切线方程,导数的运算
专题：计算题,导数的概念及应用
分析：求导函数，确定切点处的斜率与切点的坐标，即可求得函数f（x）的图象在点（1，f（1））处的切线方程．
解答：
解：∵函数f（x）=x3+f′（1）x2-x
∴f′（x）=3x2+2f′（1）x-1，
∴f′（1）=3+2f′（1）-1，
∴f′（1）=-2．
∴f（x）=x3-2x2-x，
∴f（1）=1-2-1=-2，
∴函数f（x）的图象在点（1，f（1））处的切线方程是y-（-2）=-2（x-1）
故答案为：2x+y=0．
∴f′（x）=3x2+2f′（1）x-1，
∴f′（1）=3+2f′（1）-1，
∴f′（1）=-2．
∴f（x）=x3-2x2-x，
∴f（1）=1-2-1=-2，
∴函数f（x）的图象在点（1，f（1））处的切线方程是y-（-2）=-2（x-1）
故答案为：2x+y=0．
点评：本题考查导数知识的运用，考查导数的几何意义，确定切点处的斜率与切点的坐标是关键．
练习册系列答案
相关题目
命题P：?x∈R，ax2+ax+1≥0为真命题，则实数a的取值范围是（ ）
| A、（0，4] |
| B、（-∞，4）∪（4，+∞） |
| C、（-∞，0]∪[4，+∞） |
| D、[0，4] |
函数y=
（a＜0且a为常数）在区间（-∞，1]上有意义，则实数a的取值范围（ ）
| ax+1 |
| A、[-1，0） |
| B、（-1，0） |
| C、[-1，0] |
| D、（-1，+∞） |
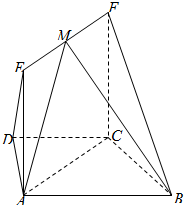如图，在梯形ABCD中，AB∥CD，AD=DC=CB=2，∠CBA=30°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=3．
正四棱锥S-ABCD中，底面正方形ABCD的边长为a，侧棱长为2a，M为SA中点，N为棱SC中点，求异面直线DM与BN所成角的余弦值．正方体ABCD-A1B1C1D1中，E，F分别是棱AD，AA1的中点，则D1E和B1F所成的角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|