题目内容
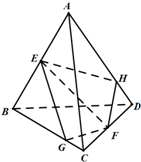如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面α分别与直线BC，AD相交于点G，H，有下列三个结论，其中正确的个数是（ ）①对于任意的平面α，都有直线GF，EH，BD相交于同一点；
②存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长
线上；
③对于任意的平面α，它把三棱锥的体积分成相等的两部分．
| A、0 | B、1 | C、2 | D、3 |
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：①取AD的中点H，BC的中点G，利用特殊值法即可判断；
②不存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长线上；
③对于任意的平面α，当G，H在线段BC，AD上时，可以证明几何体AC-EGFH的体积是四面体ABCD体积的一半．
②不存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长线上；
③对于任意的平面α，当G，H在线段BC，AD上时，可以证明几何体AC-EGFH的体积是四面体ABCD体积的一半．
解答：
解：①取AD的中点H，BC的中点G，则EGFH在一个平面内，此时直线GF∥EH∥BD，因此不正确；
②不存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长线上；
③对于任意的平面α，当G，H在线段BC，AD上时，可以证明几何体AC-EGFH的体积是四面体ABCD体积的一半，故③正确．
综上可知：只有③正确．
故选：B
②不存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长线上；
③对于任意的平面α，当G，H在线段BC，AD上时，可以证明几何体AC-EGFH的体积是四面体ABCD体积的一半，故③正确．
综上可知：只有③正确．
故选：B
点评：本题考查了线面平行的判定与性质、共面公理、三角形的中位线定理，考查了推理能力和空间想象能力，属于难题．
练习册系列答案
相关题目
i是虚数单位，复数
=（ ）
| 2-3i |
| 1-2i |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是导函数y=f′（x）的图象，则下列命题错误的是（ ）
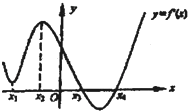
| A、导函数y=f′（x）在x1处有极小值 |
| B、导函数y=f′（x）在x2处有极大值 |
| C、导函数y=f（x）在x3处有极小值 |
| D、导函数y=f（x）在x4处有极小值 |
设-5＜a＜5，集合M={x∈N|2x-（a+5）x-10=0}．若M≠?，则满足条件的所有实数a的和等于（ ）
A、-
| ||
B、-
| ||
C、
| ||
| D、4 |