题目内容
函数f(x)=
的定义域为 .
| 1 | ||
|
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:要使函数有意义,则需x>0,且log2x-1>0,运用对数函数的单调性,即可得到定义域.
解答:
解:要使函数有意义,则需
x>0,且log2x-1>0,
即x>0且x>2,即有x>2.
则定义域为(2,+∞).
故答案为:(2,+∞).
x>0,且log2x-1>0,
即x>0且x>2,即有x>2.
则定义域为(2,+∞).
故答案为:(2,+∞).
点评:本题考查函数的定义域的求法,注意对数的真数必须大于0,偶次根式被开方式非负,分式分母不为0,考查对数函数的单调性,属于基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
设a是实数,且
+
(i是虚数单位)是实数,则a=( )
| 1+i |
| i |
| ai |
| 1-i |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
 第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )
第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )| A、甲、乙两人单场得分的最高分都是9分 |
| B、甲、乙两人单场得分的中位数相同 |
| C、甲运动员的得分更集中,发挥更稳定 |
| D、乙运动员的得分更集中,发挥更稳定. |
i是虚数单位,计算
+
=( )
| 1-i |
| 1+i |
| 1+i |
| 1-i |
| A、-2i | B、0 | C、1 | D、2i |
已知集合A={x|x+3>0},则∁RA=( )
| A、(-∞,-3) |
| B、(-∞,-3] |
| C、(-3,+∞) |
| D、[-3,+∞) |
我国的人口普查每十年进行一次,在第五次(2000年11月1日开始)人口普查时我国人口约为13亿,并发现我国人口的年平均增长率约为1%,如果按照这种速度增长,在我国开始第七次(2020年11月1日开始)普查时的人口数约为( )亿.
| A、13(1+20×1%) |
| B、13(1+19×1%) |
| C、13(1+1%)20 |
| D、13(1+1%)19 |
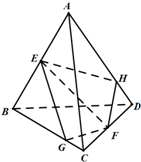 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,有下列三个结论,其中正确的个数是( )
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,有下列三个结论,其中正确的个数是( )