题目内容
7.设$a={2^{-\frac{1}{3}}},b={log_2}\frac{1}{3},c={log_{\frac{1}{2}}}\frac{1}{3}$,则( )| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
分析 利用指数函数、对数函数的单调性求解.
解答 解:∵$a={2^{-\frac{1}{3}}},b={log_2}\frac{1}{3},c={log_{\frac{1}{2}}}\frac{1}{3}$,
∴0<a=${2}^{-\frac{1}{3}}$<20=1,
$b=lo{g}_{2}\frac{1}{3}$<log21=0,
c=$lo{g}_{\frac{1}{2}}\frac{1}{3}$>$lo{g}_{\frac{1}{2}}\frac{1}{2}=1$,
∴b<a<c.
故选:C.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意指数函数、对数函数的单调性的合理运用.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
15.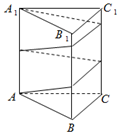 已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为4cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )
已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为4cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )
 已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为4cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )
已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为4cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )| A. | 4$\sqrt{10}$cm | B. | 12$\sqrt{3}$cm | C. | 2$\sqrt{13}$cm | D. | 13cm |