已知正三棱柱ABC-A1B1C1的底面边长为2cm.高为4cm.则一质点自点A出发.沿着三棱柱的侧面.绕行两周到达点A1的最短路线的长为( )A．4$\sqrt{10}$cmB．12$\sqrt{3}$cmC．2$\sqrt{13}$cmD．13cm 题目和参考答案——青夏教育精英家教网——

题目内容

15．

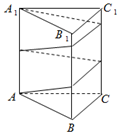已知正三棱柱ABC-A₁B₁C₁的底面边长为2cm，高为4cm，则一质点自点A出发，沿着三棱柱的侧面，绕行两周到达点A₁的最短路线的长为（　　）

A．

4$\sqrt{10}$cm

B．

12$\sqrt{3}$cm

C．

2$\sqrt{13}$cm

D．

13cm

分析将三棱柱展开，不难发现最短距离是3个矩形对角线的连线，正好相当于绕三棱柱转1次的最短路径．

解答解：将正三棱柱ABC-A₁B₁C₁沿侧棱展开，在展开图中，最短距离是6个矩形对角线的连线的长度，也即为三棱柱的侧面上所求距离的最小值．
由已知求得矩形的长等于12，宽等于4，由勾股定理d=$\sqrt{144+16}$=4$\sqrt{10}$．
故选：A．

点评本题考查棱柱的结构特征，空间想象能力，几何体的展开与折叠，体现了转化（空间问题转化为平面问题，化曲为直）的思想方法．

练习册系列答案

精彩考评单元测评卷系列答案

导学案快乐学习系列答案

孟建平各地期末试卷精选系列答案

名师三导学练考系列答案

轻松小卷系列答案

提分百分百检测卷系列答案

权威考卷系列答案

密码大考卷系列答案

宝贝计划期末冲刺夺100分系列答案

能考试全能100分系列答案

相关题目

5．若直线$y=kx+\sqrt{2}$与圆x²+y²=1没有公共点，则此直线倾斜角α的取值范围是[0，$\frac{π}{4}$）∪（$\frac{3π}{4}$，π）．

6．设集合U={1，2，3，4，5，6}，M={2，3，4}，N={4，5}，则M∪N={2，3，4，5}，∁_UM={1，5，6}．

3．若函数$f（x）=\left\{\begin{array}{l}-{x}^{2}+1，x≤1\\ x-1，x＞1\end{array}\right.$，则满足方程f（a+1）=f（a）的实数a的值为-$\frac{1}{2}$，或$\frac{-1+\sqrt{5}}{2}$．

10．函数f（x）=$\sqrt{2-{2}^{x}}$+$\frac{1}{lnx}$的定义域为（0，1）．

20．写出命题“若a²＞b²，则|a|＞|b|”的逆命题若|a|＞|b|，则a²＞b²．

7．在平面直角坐标xOy中，已知A（1，0），B（4，0），圆（x-a）²+y²=1上存在唯一的点P满足$\frac{PA}{PB}=\frac{1}{2}$，则实数a的取值集合是{-3，-1，1，3}．

6．函数$f（x）=\frac{1}{{ln（{3x+1}）}}$的定义域是（　　）

$（{-\frac{1}{3}，+∞}）$

$（{-\frac{1}{3}，0}）∪（{0，+∞}）$

$[{-\frac{1}{3}，+∞}）$

7．设$a={2^{-\frac{1}{3}}}，b={log_2}\frac{1}{3}，c={log_{\frac{1}{2}}}\frac{1}{3}$，则（　　）