题目内容
已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,那么f(19),f(63),f(16)大小关系是 .
考点:抽象函数及其应用
专题:函数的性质及应用
分析:先由“f(x)是奇函数且f(x-4)=-f(x)”转化得到f(x-8)=f(x),即函数f(x)为周期8的周期函数,然后按照条件,将问题转化到区间[0,2]上应用函数的单调性进行比较.
解答:
解:∵f(x)是奇函数且f(x-4)=-f(x),
∴f(x-8)=-f(x-4)=f(x),f(0)=0
∴函数f(x)为周期8的周期函数,
∴f(19)=f(16+3)=f(3)=f(-4+1)=f(1),
f(63)=f(64-1)=f(-1)=-f(1)
f(16)=f(0)=0,
又∵函数在区间[0,2]上是增函数
0=f(0)<f(1)
∴-f(1)<f(0)<f(1)
∴f(63)<f(16)<f(19)
故答案为:f(63)<f(16)<f(19)
∴f(x-8)=-f(x-4)=f(x),f(0)=0
∴函数f(x)为周期8的周期函数,
∴f(19)=f(16+3)=f(3)=f(-4+1)=f(1),
f(63)=f(64-1)=f(-1)=-f(1)
f(16)=f(0)=0,
又∵函数在区间[0,2]上是增函数
0=f(0)<f(1)
∴-f(1)<f(0)<f(1)
∴f(63)<f(16)<f(19)
故答案为:f(63)<f(16)<f(19)
点评:本题主要考查函数奇偶性周期性和单调性的综合运用,综合性较强,条件间结合与转化较大,属中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积是( )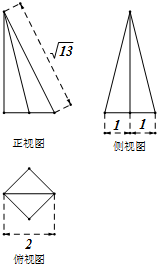

| A、2 | ||||
B、3
| ||||
C、3
| ||||
D、3
|
双曲线
-
=1的焦点到渐近线的距离为( )
| x2 |
| 4 |
| y2 |
| 12 |
A、2
| ||
| B、2 | ||
C、
| ||
| D、1 |