题目内容
设cos（
+x）=
，
＜x＜
，求
的值．
| π |
| 4 |
| 3 |
| 5 |
| 17π |
| 12 |
| 7π |
| 4 |
| 2sinxcosx+2sin2x |
| 1-tanx |
考点：两角和与差的余弦函数,三角函数的化简求值
专题：三角函数的求值
分析：由已知可得cosx-sinx=
，平方可得sinxcosx=
，进而可得cosx+sinx=-
，而原式=
，整体代入化简可得．
3
| ||
| 5 |
| 7 |
| 50 |
4
| ||
| 5 |
| 2sinxcosx(cosx+sinx) |
| cosx-sinx |
解答：
解：∵cos（
+x）=
，∴
（cosx-sinx）=
，
∴cosx-sinx=
，平方可得1-2sinxcosx=
，
∴sinxcosx=
，∴（cosx+sinx）2=1+2sinxcosx=
，
又
＜x＜
，∴
＜x+
＜2π，
∴cosx+sinx=
sin（x+
）＜0
∴cosx+sinx=-
，
∴
=
=
=-
| π |
| 4 |
| 3 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
∴cosx-sinx=
3
| ||
| 5 |
| 18 |
| 25 |
∴sinxcosx=
| 7 |
| 50 |
| 32 |
| 25 |
又
| 17π |
| 12 |
| 7π |
| 4 |
| 5π |
| 3 |
| π |
| 4 |
∴cosx+sinx=
| 2 |
| π |
| 4 |
∴cosx+sinx=-
4
| ||
| 5 |
∴
| 2sinxcosx+2sin2x |
| 1-tanx |
| 2sinx(cosx+sinx) | ||
1-
|
=
| 2sinxcosx(cosx+sinx) |
| cosx-sinx |
| 28 |
| 75 |
点评：本题考查三角函数求值，涉及两角和与差的三角函数公式，属基础题．
练习册系列答案
相关题目
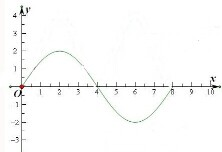已知函数f（x）=Asinωx（A＞0，ω＜0）的部分图象如图所示，则函数f（x）是（ ）| A、周期为8的偶函数 |
| B、周期为8的奇函数 |
| C、周期为8π的偶函数 |
| D、周期为8π的奇函数 |