题目内容
13．设正项等比数列{an}的前n项和为Sn，且$\frac{{{a_{n+1}}}}{a_n}＜1$，若a3+a5=20，a2a6=64，则S4=（ ）| A． | 63或126 | B． | 252 | C． | 120 | D． | 63 |
分析 设正项等比数列{an}公比为q，且0＜q=$\frac{{{a_{n+1}}}}{a_n}＜1$，根据a3+a5=20，a2a6=64=a3a5，解得a3=16，a5=4．可得q2=$\frac{1}{4}$，0＜q＜1，解得q，a1，利用求和公式即可得出．
解答 解：设正项等比数列{an}公比为q，且0＜q=$\frac{{{a_{n+1}}}}{a_n}＜1$，
∵a3+a5=20，a2a6=64=a3a5，
解得a3=16，a5=4．
∴q2=$\frac{1}{4}$，0＜q＜1，解得q=$\frac{1}{2}$，
∴${a}_{1}×\frac{1}{4}$=16，解得a1=64．
则S4=$\frac{64[1-（\frac{1}{2}）^{4}]}{1-\frac{1}{2}}$=120．
故选：C．
点评 本题考查了等比数列的通项公式与求和公式、单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
3．已知i是虚数单位，则复数$\frac{3+i}{1-i}$在复平面内所对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
4．
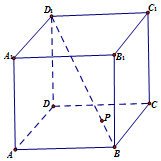正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$，动点P在对角线BD1上，过点P作垂直于BD1的平面α，平面α截正方体的表面得到一个多边形，记这样得到的截面多边形（含三角形）的周长为y，设BP=x，当$x∈[{\frac{1}{3}，\frac{5}{2}}]$时，函数y=f（x）的值域为（ ）
正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$，动点P在对角线BD1上，过点P作垂直于BD1的平面α，平面α截正方体的表面得到一个多边形，记这样得到的截面多边形（含三角形）的周长为y，设BP=x，当$x∈[{\frac{1}{3}，\frac{5}{2}}]$时，函数y=f（x）的值域为（ ）| A． | [1，3] | B． | [$\sqrt{6}$，3$\sqrt{6}$] | C． | [$\frac{3\sqrt{6}}{2}$，4$\sqrt{6}$] | D． | [$\sqrt{6}$，4$\sqrt{6}$] |
1．下列函数中，最小正周期为π的偶函数是（ ）
| A． | y=sinx+cosx | B． | y=cos4x-sin4x | C． | y=cos|x| | D． | y=$\frac{tanx}{1-ta{n}^{2}x}$ |
如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为$\frac{{\sqrt{2}}}{10}$，$\frac{{2\sqrt{5}}}{5}$．
18．8个不同的球放入三个相同的盒子中，问有多少种不同的放法？（ ）
| A． | 1094 | B． | 966 | C． | 5796 | D． | 6561 |
5．若向量$\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（1，-1），$\overrightarrow{c}$=（-1，2），则c=（ ）
| A． | $\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B． | -$\frac{3}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C． | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$ | D． | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$ |
如图，四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PD=CD=2，∠PDC=120°．