题目内容
11.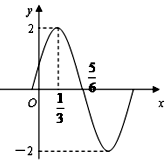 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是f(x)=2sin(πx+$\frac{π}{6}$),x∈R.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是f(x)=2sin(πx+$\frac{π}{6}$),x∈R.
分析 根据函数图象可得周期T、振幅A,利用周期公式求出ω,
利用解析式及φ的范围求出φ的值,即可确定函数解析式.
解答 解:∵根据图象判断,周期为
T=4×($\frac{5}{6}$-$\frac{1}{3}$)=2,A=2,
∴$\frac{2π}{ω}$=2,解得:ω=π;
又2sin(π×$\frac{1}{3}$+φ)=2,
∴$\frac{π}{3}$+φ=2kπ+$\frac{π}{2}$,k∈z,
∴φ=2kπ+$\frac{π}{6}$,k∈z;
又|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$;
∴f(x)的解析式为f(x)=2sin(πx+$\frac{π}{6}$),x∈R.
故答案为:f(x)=2sin(πx+$\frac{π}{6}$),x∈R.
点评 本题考查了由y=Asin(ωx+φ)的部分图象确定其解析式的应用问题,是基础题.

练习册系列答案
相关题目
19.设点P圆C:x2+y2=1上的一个动点,则点P到直线x+$\sqrt{3}$y-4=0的距离最小值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
6.过双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右顶点A作斜率为-1的直线,该直线与E的渐近线交于B,C两点,若$\overrightarrow{BC}+2\overrightarrow{BA}$=$\overrightarrow 0$,则双曲线E的渐近线方程为( )
| A. | y=±$\sqrt{3}$x | B. | y=±4x | C. | y=±$\sqrt{2}$x | D. | y=±2x |
3.记sin(-80°)=k,那么tan100°=( )
| A. | $\frac{{\sqrt{1-{k^2}}}}{k}$ | B. | $-\frac{{\sqrt{1-{k^2}}}}{k}$ | C. | $\frac{k}{{\sqrt{1-{k^2}}}}$ | D. | $-\frac{k}{{\sqrt{1-{k^2}}}}$ |
1.双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1的离心率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{\sqrt{41}}{5}$ | D. | $\frac{5}{\sqrt{41}}$ |