题目内容
1.双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1的离心率是( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{\sqrt{41}}{5}$ | D. | $\frac{5}{\sqrt{41}}$ |
分析 求得双曲线的a,b,c,运用e=$\frac{c}{a}$,计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1的a=5,b=4,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{41}$,
可得e=$\frac{c}{a}$=$\frac{\sqrt{41}}{5}$.
故选:C.
点评 本题考查双曲线的方程和性质,主要是离心率的求法,求得双曲线的基本量是解题的关键,属于基础题.

练习册系列答案
相关题目
12.已知直线m、l与平面α、β、γ满足β∩γ=l,l∥α,m?α,m⊥γ,则下列命题一定正确的是( )
| A. | α⊥γ且l⊥m | B. | α⊥γ且m∥β | C. | m∥β且l⊥m | D. | α∥β且α⊥γ |
6.sin(-$\frac{10π}{3}$)的值是( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
13.设x,y,z均为正实数,a=x+$\frac{1}{y}$,b=y+$\frac{1}{z}$,c=z+$\frac{1}{x}$,则a,b,c三个数( )
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
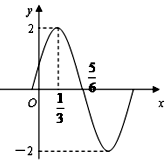 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是f(x)=2sin(πx+$\frac{π}{6}$),x∈R.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是f(x)=2sin(πx+$\frac{π}{6}$),x∈R.