题目内容
3.记sin(-80°)=k,那么tan100°=( )| A. | $\frac{{\sqrt{1-{k^2}}}}{k}$ | B. | $-\frac{{\sqrt{1-{k^2}}}}{k}$ | C. | $\frac{k}{{\sqrt{1-{k^2}}}}$ | D. | $-\frac{k}{{\sqrt{1-{k^2}}}}$ |
分析 先利用同角三角函数的基本关系式以及诱导公式求cos80°,然后化切为弦,即可求得tan100°.
解答 解:∵sin(-80°)=k,∴sin80°=-k,
∴cos80°=$\sqrt{1-si{n}^{2}80°}=\sqrt{1-{k}^{2}}$,
∴tan100°=-tan80°=$-\frac{sin80°}{cos80°}=-\frac{-k}{\sqrt{1-{k}^{2}}}=\frac{k}{\sqrt{1-{k}^{2}}}$.
故选:C.
点评 本题主要考查诱导公式、同角三角函数关系式等三角函数知识,并突出了弦切互化这一转化思想的应用,是基础题.

练习册系列答案
相关题目
8.已知扇形的圆心角是72°,半径为20cm,则扇形的面积为( )
| A. | 70πcm2 | B. | 70 cm2 | C. | 80cm2 | D. | 80πcm2 |
15.如果$\overrightarrow{e_1}$,$\overrightarrow{e_2}$是平面内所有向量的一组基底,那么( )
| A. | 该平面内存在一向量$\overrightarrow a$不能表示$\overrightarrow a=m\overrightarrow{e_1}+n\overrightarrow{e_2}$,其中m,n为实数 | |
| B. | 若向量$m\overrightarrow{e_1}+n\overrightarrow{e_2}$与$\overrightarrow a$共线,则存在唯一实数λ使得$m\overrightarrow{e_1}+n\overrightarrow{e_2}=λ\overrightarrow a$ | |
| C. | 若实数m,n使得$m\overrightarrow{e_1}+n\overrightarrow{e_2}=\overrightarrow 0$,则m=n=0 | |
| D. | 对平面中的某一向量$\overrightarrow a$,存在两对以上的实数m,n使得$\overrightarrow a=m\overrightarrow{e_1}+n\overrightarrow{e_2}$ |
12.已知直线m、l与平面α、β、γ满足β∩γ=l,l∥α,m?α,m⊥γ,则下列命题一定正确的是( )
| A. | α⊥γ且l⊥m | B. | α⊥γ且m∥β | C. | m∥β且l⊥m | D. | α∥β且α⊥γ |
13.设x,y,z均为正实数,a=x+$\frac{1}{y}$,b=y+$\frac{1}{z}$,c=z+$\frac{1}{x}$,则a,b,c三个数( )
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
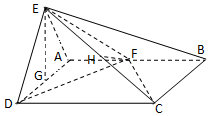 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.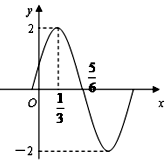 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是f(x)=2sin(πx+$\frac{π}{6}$),x∈R.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是f(x)=2sin(πx+$\frac{π}{6}$),x∈R.