题目内容
2.若P为圆(x-2)2+y2=1上的动点,则点P到直线l:x-y+2=0的最短距离为2$\sqrt{2}$-1.分析 点P到直线l:x-y+2=0的最短距离为圆心到直线距离再减去半径.
解答 解:点P到直线l:x-y+2=0的最短距离为圆心到直线距离再减去半径.
圆(x-2)2+y2=1圆心为(2,0),
则圆心(2,0)到直线l:x-y+2=0的距离为d=$\frac{|2+2|}{\sqrt{2}}$=2$\sqrt{2}$,
半径为r=1,
故点P到直线l:x-y+2=0的最短距离为2$\sqrt{2}$-1.
故答案为:2$\sqrt{2}$-1.
点评 本题考查点到直线的最短距离的求法,考查圆的性质、直线与圆的位置关系,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
12.已知直线m、l与平面α、β、γ满足β∩γ=l,l∥α,m?α,m⊥γ,则下列命题一定正确的是( )
| A. | α⊥γ且l⊥m | B. | α⊥γ且m∥β | C. | m∥β且l⊥m | D. | α∥β且α⊥γ |
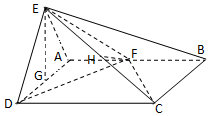 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.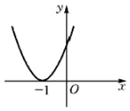
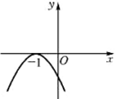
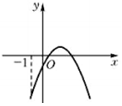
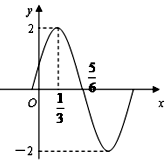 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是f(x)=2sin(πx+$\frac{π}{6}$),x∈R.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是f(x)=2sin(πx+$\frac{π}{6}$),x∈R.