题目内容
已知△ABC的周长为4(
+1),且sinB+sinC=
sinA.
(1)求边长a的值;
(2)若S△ABC=3sinA,求角A的大小(结果用反三角函数值表示).
| 2 |
| 2 |
(1)求边长a的值;
(2)若S△ABC=3sinA,求角A的大小(结果用反三角函数值表示).
考点:正弦定理,反三角函数的运用
专题:解三角形
分析:(1)利用正弦定理,将角转化为边之间的关系,利用周长即可求出a的值.
(2)利用三角形的面积公式,求出b,c的关系,利用余弦定理即可求出A的大小.
(2)利用三角形的面积公式,求出b,c的关系,利用余弦定理即可求出A的大小.
解答:
解:(1)∵sinB+sinC=
sinA,
∴由正弦定理得,b+c=
a,(*)
∵a+b+c=4(
+1),
∴解得a=4;
(2)由S△ABC=
bcsinA=3sinA,得bc=6,
两边平方(*)式,求得b2+c2=20,
由余弦定理,cosA=
=
=
=
,
故A=arccos
.
| 2 |
∴由正弦定理得,b+c=
| 2 |
∵a+b+c=4(
| 2 |
∴解得a=4;
(2)由S△ABC=
| 1 |
| 2 |
两边平方(*)式,求得b2+c2=20,
由余弦定理,cosA=
| b2+c2-a2 |
| 2bc |
| 20-16 |
| 2×6 |
| 4 |
| 12 |
| 1 |
| 3 |
故A=arccos
| 1 |
| 3 |
点评:本题主要考查正弦定理和余弦定理的应用,要求熟练掌握正弦定理和余弦定理.

练习册系列答案
相关题目
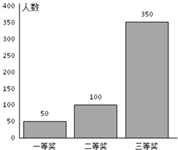 某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示.消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题.
某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示.消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题.