题目内容
定义在R上的函数f(x)满足f(x)=
,则f(2013)的值为 .
|
考点:抽象函数及其应用,函数的值
专题:函数的性质及应用
分析:利用当x>0时的条件,推导出函数是周期函数,然后利用周期函数进行求值即可.
解答:
解:当x>0时,f(x)=f(x-1)-f(x-2),
则f(x+1)=f(x)-f(x-1),
则两式联立得f(x+1)=-f(x-2),
即f(x+3)=-f(x),所以f(x+6)=f(x).
即此时函数的周期为6,(x>0时).
所以f(2013)=f(335×6+3)=f(3),
因为f(3)=f(2)-f(1)=f(1)-f(0)-f(1)=-f(0)=-log24=-2,
所以f(2013)=f(3)=-2,
故答案为:-2.
则f(x+1)=f(x)-f(x-1),
则两式联立得f(x+1)=-f(x-2),
即f(x+3)=-f(x),所以f(x+6)=f(x).
即此时函数的周期为6,(x>0时).
所以f(2013)=f(335×6+3)=f(3),
因为f(3)=f(2)-f(1)=f(1)-f(0)-f(1)=-f(0)=-log24=-2,
所以f(2013)=f(3)=-2,
故答案为:-2.
点评:本题主要考查函数周期性的判断和应用,利用条件推导出函数的周期性是解决本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
函数f(x)=sin(2x+
)是由f(x)=sin2x的图象经过怎样的平移变换得到的( )
| π |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
函数的图象如图所示,为了得到的图象,则只要将f(x)=cos2x的函数的图象( )
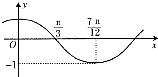

A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
在映射f:A→B中,A=B=R,且f:(x,y)→(x-y,x+y),则与A中的元素(2,1)在B中的象为( )
| A、(-3,1) |
| B、(1,3) |
| C、(-1,-3) |
| D、(3,1) |