题目内容
设直线l：x-y+m=0与抛物线C：y2=4x交于不同两点A、B，F为抛物线的焦点，则△ABF的重心G的轨迹的普通方程为 ．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：设出A、B、G的坐标，联立直线与抛物线，利用重心坐标公式，即可求得重心G的轨迹方程．
解答：
解：设A（x1，y1），B（x2，y2），F（1，0），重心G（x，y），
联立直线与抛物线，消元可得y2-4y+4m=0
∴△＞0⇒m＜1且m≠-1（因为A、B、F不共线）
故x=
=
=
，y=
=
∴重心G的轨迹方程为y=
(x＞1且x≠
)．
故答案为：y=
(x＞1且x≠
)．
联立直线与抛物线，消元可得y2-4y+4m=0
∴△＞0⇒m＜1且m≠-1（因为A、B、F不共线）
故x=
| x2+x2+1 |
| 3 |
| y1+y2-2m+1 |
| 3 |
| 5-2m |
| 3 |
| y1+y2 |
| 3 |
| 4 |
| 3 |
∴重心G的轨迹方程为y=
| 4 |
| 3 |
| 7 |
| 3 |
故答案为：y=
| 4 |
| 3 |
| 7 |
| 3 |
点评：本题考查轨迹方程，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
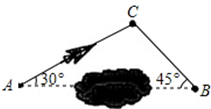一架飞机从马来西亚吉隆坡飞往中国北京，两地相距4500km．飞行员为了避开某一区域的雷雨云层，从机场起飞以后，就沿与原来的飞行方向成30°角的方向飞行，飞行到途中，再沿与原来的飞行方向成45°角的方向继续飞行直到终点．这样飞机的飞行路程比原来的路程4500km远了多少？（参考数据：已知函数f（x）=（sinx+cosx）2-2sin2x-m在[0，
]上有两个零点，则实数m的取值范围是（ ）
| π |
| 2 |
A、[1，
| ||
B、[1，
| ||
C、（1，
| ||
| D、[1，+∞） |