题目内容
设向量
，
是同一平面内所有向量的一组基底，若（λ
+
）∥（
-2
），则实数λ的值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：利用向量共线定理和平面向量基本定理即可得出．
解答：
解：∵（λ
+
）∥（
-2
），
∴存在实数k使得λ
+
=k(
-2
)，
化为(λ-k)
+(1+2k)
=
，
∵向量
，
是同一平面内所有向量的一组基底，
∴
，解得λ=k=-
．
故选：D．
| a |
| b |
| a |
| b |
∴存在实数k使得λ
| a |
| b |
| a |
| b |
化为(λ-k)
| a |
| b |
| 0 |
∵向量
| a |
| b |
∴
|
| 1 |
| 2 |
故选：D．
点评：本题考查了向量共线定理和平面向量基本定理，属于基础题．
练习册系列答案
相关题目
若复数z满足z•（1-i）=2-i（其中i是虚数单位），则z=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若tanθ=
，则
=（ ）
| 3 |
| sin2θ |
| 1+cos2θ |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若直线y=|
|x+1与直线y=|
|x平行，
，
为非零向量，则必有（ ）
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、（
| ||||||||
D、（
|
将函数y=sin2x+
cos2x（x∈R）的图象向右平移m（m＞0）个单位长度后，所得到的图象关于原点对称，则m的最小值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是（ ）
| A、“a＞b”是“a2＞b2”的充分不必要条件 |
| B、命题“?x0∈R，x02+1＜0”的否定是：“?x∈R，x2+1＞0” |
| C、关于x的方程x2+（a+1）x+a-2=0的两根异号的充要条件是a＜1 |
| D、若f（x）为R上的偶函数，则f（x-1）的图象关于直线x=1对称 |
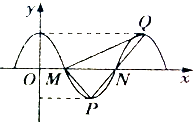已知函数f（x）=Acosωx（ω＞0）的部分图象如图所示，且∠MQP=