题目内容
12.(1)求函数y=x2-4x+5,x∈[0,5)的值域;(2)已知函数f(x)=$\frac{x-1}{x+2}$,x∈[3,5]求函数f(x)的最大值和最小值.
分析 (1)求出f(x)的对称轴x=2,可得f(2)最小,再由f(0),f(5)可得最大值,进而得到值域;
(2)求得f(x)=1-$\frac{3}{x+2}$,可得f(x)在[3,5]递增,即可得到f(x)的最值.
解答 解:(1)函数y=x2-4x+5=(x-2)2+1的对称轴为x=2,
即有x=2∈[0,5],取得最小值1;
当x=0时,f(0)=5;当x=5时,f(5)=10.
则f(x)是最大值为10.
即有函数f(x)的值域为[1,10];
(2)函数f(x)=$\frac{x-1}{x+2}$=1-$\frac{3}{x+2}$,
可得f(x)在[3,5]递增,
即有f(3)为最小值,且为$\frac{2}{5}$;
f(5)取得最大值,且为$\frac{4}{7}$.
点评 本题考查函数的值域和最值的求法,注意运用函数的单调性,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知直线m过双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的左焦点F1,且与该双曲线的左支交于A,B两点,若|AB|=2,双曲线的右焦点为F2,则△ABF2的周长为( )
| A. | 6 | B. | 8 | C. | 12 | D. | 20 |
7.已知椭圆的焦点为F1(0,-1),F2(0,1),且经过点M($\frac{7}{4}$,$\frac{3\sqrt{2}}{2}$),则椭圆的方程为( )
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 | C. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{8}$=1 |
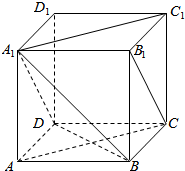 如图在正方体ABCD-A1B1C1D1中,
如图在正方体ABCD-A1B1C1D1中,