题目内容
2.已知PA⊥面ABCD,PA=AB=3,面ABCD为正方形.试建立适当的平面直角坐标系,分别求下列平面的法向量.(1)面ABCD;
(2)面PAB;
(3)面PBC;
(4)面PCD.
分析 利用线面垂直的性质、向量垂直与数量积的关系即可得出.
解答 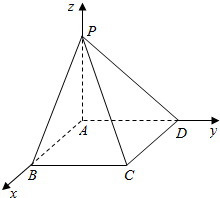 解:如图所示,建立空间直角坐标系.
解:如图所示,建立空间直角坐标系.
则(1)面ABCD的法向量为(0,0,1);
(2)面PAB的法向量为(0,1,0);
(3)由B(3,0,0),C(3,3,0),P(0,0,3).
∴$\overrightarrow{PB}$=(3,0,-3),$\overrightarrow{PC}$=(3,3,-3),
设平面PBC是法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=0}\\{\overrightarrow{n}•\overrightarrow{PC}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{3x-3z=0}\\{3x+3y-3z=0}\end{array}\right.$,取$\overrightarrow{n}$=(1,0,1);
(4)由(3)同理可得:平面PCD的法向量为:$\overrightarrow{m}$=(0,1,1).
点评 本题考查了线面垂直的性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1的焦点在y轴上,则一定有( )
| A. | m>n>0 | B. | n>m>0 | C. | 0>m>n | D. | 0>n>m |
17.下列命题为真命题的是( )
| A. | 质数中没有偶数 | B. | 空集没有真子集 | ||
| C. | 若原命题为真,则否命题为假 | D. | 面积相等的三个三角形全等 |