题目内容
设l为直线,α,β是两个不同的平面,下列命题中正确的是( )
| A、若l∥α,l∥β,则α∥β |
| B、若α∥β,l∥α,则l∥β |
| C、若l⊥α,l∥β,则α⊥β |
| D、若α⊥β,l∥α,则l⊥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:借助于长方体中的线面关系直观判断,恰当选取长方体中的线与面来表示题目中涉及到的线、面,然后进行判断.
解答:
解:对于A项,在长方体中,任何一条棱都有和它相对的两个平面平行,但这两个平面相交,所以A不对;
对于B项,若α、β分别是长方体的上下底面,在下底面所在平面中任选一条直线l,都有l∥α,但l?β,所以B不对;
对于D项,在长方体中,令下底面为β,左边侧面为α,此时α⊥β,在右边侧面中取一条对角线l,则l∥α,但l与β不垂直,故D不对;
对于C项,设平面γ∩β=m,且l?γ,∵l∥β,所以l∥m,又∵l⊥α,所以m⊥α,由γ∩β=m得m?β,∴α⊥β.
故选C
对于B项,若α、β分别是长方体的上下底面,在下底面所在平面中任选一条直线l,都有l∥α,但l?β,所以B不对;
对于D项,在长方体中,令下底面为β,左边侧面为α,此时α⊥β,在右边侧面中取一条对角线l,则l∥α,但l与β不垂直,故D不对;
对于C项,设平面γ∩β=m,且l?γ,∵l∥β,所以l∥m,又∵l⊥α,所以m⊥α,由γ∩β=m得m?β,∴α⊥β.
故选C
点评:在选择题中考查空间线面关系中的平行与垂直关系的判断问题,一般会借助于长方体中的线面来直观判断.

练习册系列答案
相关题目
设正弦函数f(x)=cosx在x=0和x=
处得切线得斜率分别为k1,k2,则k1,k2的大小关系为( )
| π |
| 2 |
| A、k1<k2 |
| B、k1>k2 |
| C、k1=k2 |
| D、不确定 |
现有等腰三角形纸片ABC,∠A=90°,BC=2,按图示方式剪下两个正方形,则这两个正方形的面积之和的最小值为( )
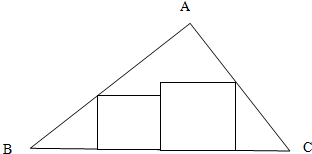

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
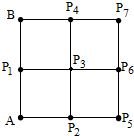 如图,四个边长为1的小正方形排成一个大正方形,AB是大正方形的一条边,Pi(i=1,2,…,7)是小正方形的其余顶点,则
如图,四个边长为1的小正方形排成一个大正方形,AB是大正方形的一条边,Pi(i=1,2,…,7)是小正方形的其余顶点,则| AB |
| APi |
| A、7 | B、5 | C、3 | D、1 |
若3a,b,c成等比数列,则函数f(x)=ax3+bx2+cx+d的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |
