题目内容
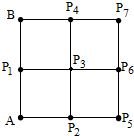如图，四个边长为1的小正方形排成一个大正方形，AB是大正方形的一条边，Pi（i=1，2，…，7）是小正方形的其余顶点，则| AB |
| APi |
| A、7 | B、5 | C、3 | D、1 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：建立适当的平面直角坐标系，利用坐标分别求出数量积，由结果可得答案．
解答：
解：如图建立平面直角坐标系，
则A（0，0），B（0，2），P1（0，1），P2（1，0），P3（1，1），P4（1，2），P5（2，0），P6（2，1），P7（2，2），
∴
=(0，2)，
=（0，1），
=（1，0），
=（1，1），
=（1，2），
=（2，0），
=（2，1），
=（2，2），
∴
•
=2，
•
=0，
•
=2，
•
=4，
•
=0，
•
=2，
•
=4，
∴
•
（i=1，2，…，7）的不同值的个数为3，
故选C．
解：如图建立平面直角坐标系，则A（0，0），B（0，2），P1（0，1），P2（1，0），P3（1，1），P4（1，2），P5（2，0），P6（2，1），P7（2，2），
∴
| AB |
| AP1 |
| AP2 |
| AP3 |
| AP4 |
| AP5 |
| AP6 |
| AP7 |
∴
| AB |
| AP1 |
| AB |
| AP2 |
| AB |
| AP3 |
| AB |
| AP4 |
| AB |
| AP5 |
| AB |
| AP6 |
| AB |
| AP7 |
∴
| AB |
| APi |
故选C．
点评：本题考查平面向量的数量积运算，属基础题．
练习册系列答案
相关题目
设l为直线，α，β是两个不同的平面，下列命题中正确的是（ ）
| A、若l∥α，l∥β，则α∥β |
| B、若α∥β，l∥α，则l∥β |
| C、若l⊥α，l∥β，则α⊥β |
| D、若α⊥β，l∥α，则l⊥β |
双曲线
-
=1的一条渐近线的倾斜角为α，且2cos2α=2sin2α+1，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知曲线C为三次函数f（x）=3x-x3的图象，过点M（2，1）作曲线C的切线，可能的切线条数是（ ）
| A、0 | B、1 | C、2 | D、3 |
积分∫
dx=（ ）
0 |
| cos2x |
| cosx+sinx |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
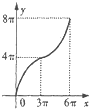
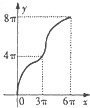
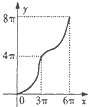
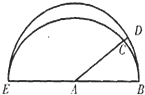如图是半径为4的半圆A与它的内切半椭圆（长半轴长为4，短半轴长为3），AD为半圆的半径，且交半椭圆于点C．现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转，设圆弧BD与AD、AB围成的面积为y，椭圆弧BC与AC、AB所围成的面积为x，则函数y=f（x）的图象大致是（ ）
球面上有三个点A、B、C，其中AB=18，BC=24，AC=30，且球心到平面ABC的距离为球半径的一半，那么这个球的半径为（ ）
| A、20 | ||
| B、30 | ||
C、10
| ||
D、15
|