题目内容
数列{an}中，若an+an+1=7n+5，n∈N*，则a1+a100= ．
考点：数列递推式
专题：计算题,点列、递归数列与数学归纳法
分析：利用a1+a100=（a1+a2）-（a2+a3）+（a3+a4）-…+（a99+a100），即可得出结论．
解答：
解：∵an+an+1=7n+5，n∈N*，
∴a1+a100=（a1+a2）-（a2+a3）+（a3+a4）-…+（a99+a100）=12+7×49=355．
故答案为：355．
∴a1+a100=（a1+a2）-（a2+a3）+（a3+a4）-…+（a99+a100）=12+7×49=355．
故答案为：355．
点评：本题考查数列递推式，考查学生的计算能力，利用a1+a100=（a1+a2）-（a2+a3）+（a3+a4）-…+（a99+a100）是关键．
练习册系列答案
相关题目
设l为直线，α，β是两个不同的平面，下列命题中正确的是（ ）
| A、若l∥α，l∥β，则α∥β |
| B、若α∥β，l∥α，则l∥β |
| C、若l⊥α，l∥β，则α⊥β |
| D、若α⊥β，l∥α，则l⊥β |
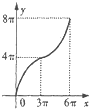
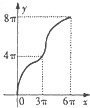
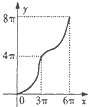
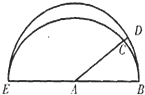如图是半径为4的半圆A与它的内切半椭圆（长半轴长为4，短半轴长为3），AD为半圆的半径，且交半椭圆于点C．现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转，设圆弧BD与AD、AB围成的面积为y，椭圆弧BC与AC、AB所围成的面积为x，则函数y=f（x）的图象大致是（ ）
