题目内容
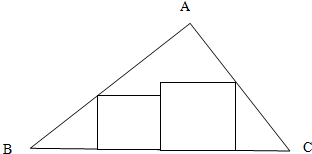
现有等腰三角形纸片ABC,∠A=90°,BC=2,按图示方式剪下两个正方形,则这两个正方形的面积之和的最小值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:根据实际问题选择函数类型
专题:函数的性质及应用
分析:设BD=x,CF=y,建立面积关系,然后利用二次函数的图象和性质即可得到结论.
解答:
 解:设BD=x,CF=y,
解:设BD=x,CF=y,
则GD=DE=x,FH=EF=y,且BD+DE+EF+FC=2,
即2x+2y=2,则x+y=1,y=1-x,(0<x<1),
则两个正方形的面积之和S=x2+y2=x2+(1-x)2=2(x-
)2+
,
则当x=
时,面积S=2(x-
)2+
取得最小值
,
故选:C
 解:设BD=x,CF=y,
解:设BD=x,CF=y,则GD=DE=x,FH=EF=y,且BD+DE+EF+FC=2,
即2x+2y=2,则x+y=1,y=1-x,(0<x<1),
则两个正方形的面积之和S=x2+y2=x2+(1-x)2=2(x-
| 1 |
| 2 |
| 1 |
| 2 |
则当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:C
点评:本题主要考查函数最值的应用,设出变量,利用二次函数的图象和性质即可得到结论.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
设l为直线,α,β是两个不同的平面,下列命题中正确的是( )
| A、若l∥α,l∥β,则α∥β |
| B、若α∥β,l∥α,则l∥β |
| C、若l⊥α,l∥β,则α⊥β |
| D、若α⊥β,l∥α,则l⊥β |
下列说法正确的是( )
A、若a∈R,则“
| ||
| B、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | ||
C、若命题p:“?x∈R,sinx+cosx≤
| ||
| D、命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3>0” |
双曲线
-
=1的一条渐近线的倾斜角为α,且2cos2α=2sin2α+1,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知曲线C为三次函数f(x)=3x-x3的图象,过点M(2,1)作曲线C的切线,可能的切线条数是( )
| A、0 | B、1 | C、2 | D、3 |
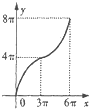
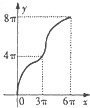
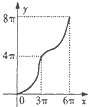
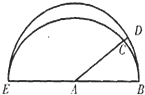 如图是半径为4的半圆A与它的内切半椭圆(长半轴长为4,短半轴长为3),AD为半圆的半径,且交半椭圆于点C.现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转,设圆弧BD与AD、AB围成的面积为y,椭圆弧BC与AC、AB所围成的面积为x,则函数y=f(x)的图象大致是( )
如图是半径为4的半圆A与它的内切半椭圆(长半轴长为4,短半轴长为3),AD为半圆的半径,且交半椭圆于点C.现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转,设圆弧BD与AD、AB围成的面积为y,椭圆弧BC与AC、AB所围成的面积为x,则函数y=f(x)的图象大致是( )