题目内容
若3a,b,c成等比数列,则函数f(x)=ax3+bx2+cx+d的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:通过对函数f(x)求导,得出导函数只有一个解,从而得出函数f(x)只有一个零点.
解答:
解:∵f′(x)=3ax2+2bx+c,
∴△=(2b)2-4•3a•c
=4(b2-3ac),
又∵3a,b,c成等比数列,
∴b2-3ac=0,
∴△=0,
∴函数f(x)=ax3+bx2+cx+d在R上单调,
∴函数f(x)有且只有一个零点,
故选:B.
∴△=(2b)2-4•3a•c
=4(b2-3ac),
又∵3a,b,c成等比数列,
∴b2-3ac=0,
∴△=0,
∴函数f(x)=ax3+bx2+cx+d在R上单调,
∴函数f(x)有且只有一个零点,
故选:B.
点评:本题考察了函数的零点问题,等比数列的概念,导函数的应用,是一道基础题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
设l为直线,α,β是两个不同的平面,下列命题中正确的是( )
| A、若l∥α,l∥β,则α∥β |
| B、若α∥β,l∥α,则l∥β |
| C、若l⊥α,l∥β,则α⊥β |
| D、若α⊥β,l∥α,则l⊥β |
球面上有三个点A、B、C,其中AB=18,BC=24,AC=30,且球心到平面ABC的距离为球半径的一半,那么这个球的半径为( )
| A、20 | ||
| B、30 | ||
C、10
| ||
D、15
|
设等差数列{an}的通项公式满足an=2n-7(n∈N*),则|a1|+|a2|+…+|a15|=( )
| A、130 | B、139 |
| C、153 | D、178 |
若对定义在R上的可导函数f(x)恒有(4-x)f(x)+xf′(x)>0,则f(x)( )
| A、恒大于等于0 |
| B、恒小于0 |
| C、恒大于0 |
| D、和0的大小关系不能确定 |
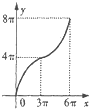
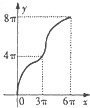
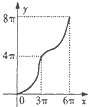
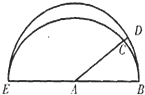 如图是半径为4的半圆A与它的内切半椭圆(长半轴长为4,短半轴长为3),AD为半圆的半径,且交半椭圆于点C.现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转,设圆弧BD与AD、AB围成的面积为y,椭圆弧BC与AC、AB所围成的面积为x,则函数y=f(x)的图象大致是( )
如图是半径为4的半圆A与它的内切半椭圆(长半轴长为4,短半轴长为3),AD为半圆的半径,且交半椭圆于点C.现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转,设圆弧BD与AD、AB围成的面积为y,椭圆弧BC与AC、AB所围成的面积为x,则函数y=f(x)的图象大致是( )