题目内容
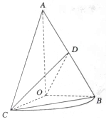 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=| π |
| 2 |
| π |
| 6 |
(1)当平面COD⊥平面AOB时,证明:OC⊥OB;
(2)若θ∈[
| π |
| 2 |
| 2π |
| 3 |
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)在平面AOB内过B作OD的垂线,垂足为H,证明BH⊥平面COD,可得BH⊥CO,又因为OC⊥AO,BH和OA相交,所以OC⊥平面AOB,从而证明OC⊥OB;
(2)VC-AOB=VA-OBC=
×
×OB×OCsinθ×2
=
sinθ,利用θ∈[
,
],即可求三棱锥C-AOB的体积V的取值范围.
(2)VC-AOB=VA-OBC=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
4
| ||
| 3 |
| π |
| 2 |
| 2π |
| 3 |
解答:
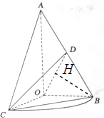 (1)证明:在平面AOB内过B作OD的垂线,垂足为H,
(1)证明:在平面AOB内过B作OD的垂线,垂足为H,
∵平面COD⊥平面AOB,平面COD∩平面AOB=OD,
又BH⊥OD,BH?平面AOB,
则BH⊥平面COD.
又由OC?平面COD,BH⊥CO,
又因为OC⊥AO,BH和OA相交,
所以OC⊥平面AOB.
又OB?平面AOB,从而OC⊥OB.
(2)解:由题意,AO是三棱锥A-OBC的高,
在直角△AOB中,AB=4,∠AOB=
,
∴AO=ABcos
=2
,OC=OB=ABsin
=2,
∴VC-AOB=VA-OBC=
×
×OB×OCsinθ×2
=
sinθ,
∵θ∈[
,
],
∴
≤sinθ≤1,
∴2≤VC-AOB≤
.
 (1)证明:在平面AOB内过B作OD的垂线,垂足为H,
(1)证明:在平面AOB内过B作OD的垂线,垂足为H,∵平面COD⊥平面AOB,平面COD∩平面AOB=OD,
又BH⊥OD,BH?平面AOB,
则BH⊥平面COD.
又由OC?平面COD,BH⊥CO,
又因为OC⊥AO,BH和OA相交,
所以OC⊥平面AOB.
又OB?平面AOB,从而OC⊥OB.
(2)解:由题意,AO是三棱锥A-OBC的高,
在直角△AOB中,AB=4,∠AOB=
| π |
| 2 |
∴AO=ABcos
| π |
| 6 |
| 3 |
| π |
| 6 |
∴VC-AOB=VA-OBC=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
4
| ||
| 3 |
∵θ∈[
| π |
| 2 |
| 2π |
| 3 |
∴
| ||
| 2 |
∴2≤VC-AOB≤
4
| ||
| 3 |
点评:本题考查的知识点是与二面角有关的立体几何问题,平面与平面垂直的性质,考查三棱锥体积的计算,属于中档题.

练习册系列答案
相关题目
若△ABC的内角满足sinA+
sinB=2sinC,则cosC的最小值是( )
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,已知正方形ABCD和ADMN边长都为2,且平面ABCD⊥平面ADMN,E是BC的中点,F是MD的中点,
如图,已知正方形ABCD和ADMN边长都为2,且平面ABCD⊥平面ADMN,E是BC的中点,F是MD的中点, 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=