题目内容
已知函数f(x)=
x3+ax2-bx(a,b∈R),若y=f(x)图象上的点(1,-
)处的切线斜率为-4,
(1)求f(x)的表达式.
(2)求y=f(x)在区间[-3,6]上的最值.
| 1 |
| 3 |
| 11 |
| 3 |
(1)求f(x)的表达式.
(2)求y=f(x)在区间[-3,6]上的最值.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)根据导数的几何意义,建立方程关系即可求f(x)的表达式.
(2)求函数的导数,利用函数的单调性和最值与导数之间的关系,即可求y=f(x)在区间[-3,6]上的最值.
(2)求函数的导数,利用函数的单调性和最值与导数之间的关系,即可求y=f(x)在区间[-3,6]上的最值.
解答:
解:(1)∵f(x)=
x3+ax2-bx,
∴f′(x)=x2+2ax-b,
∵y=f(x)图象上的点(1,-
)处的切线斜率为-4,
∴f′(1)=-4,f(1)=-
,
∴1+2a-b=-4.①,
+a-b=-
,即a-b+4=0.②
由①②解得a=-1,b=3,
∴f(x)=
x3-x2-3x.
(2)∵f(x)=
x3-x2-3x.
∴f′(x)=x2-2x-3=(x-3)(x+1).
令f′(x)=0,解得x=-1或3.
∴在x∈[-3,6]上,当x变化时,f′(x),f(x)的变化情况如下表:
∴当x∈[-3,6]时,f(x)max=f(6)=18,
f(x)min=f(3)=f(-3)=-9.
| 1 |
| 3 |
∴f′(x)=x2+2ax-b,
∵y=f(x)图象上的点(1,-
| 11 |
| 3 |
∴f′(1)=-4,f(1)=-
| 11 |
| 3 |
∴1+2a-b=-4.①,
| 1 |
| 3 |
| 11 |
| 3 |
由①②解得a=-1,b=3,
∴f(x)=
| 1 |
| 3 |
(2)∵f(x)=
| 1 |
| 3 |
∴f′(x)=x2-2x-3=(x-3)(x+1).
令f′(x)=0,解得x=-1或3.
∴在x∈[-3,6]上,当x变化时,f′(x),f(x)的变化情况如下表:
| x | -3 | (-3,-1) | -1 | (-1,3) | 3 | (3,6) | 6 | ||
| f′(x) | + | 0 | - | 0 | + | ||||
| f(x) | -9 | 单调递增↗ | 极大值
| 单调递减↘ | 极小值-9 | 单调递增↗ | 18 |
f(x)min=f(3)=f(-3)=-9.
点评:本题主要考查导数的几何意义以及函数最值的求解,利用导数在研究函数的应用时解决本题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
下列函数中,在区间(0,
)上为增函数的是( )
| π |
| 2 |
| A、y=sin2x |
| B、y=cosx |
| C、y=-cos2x |
| D、y=-tanx |
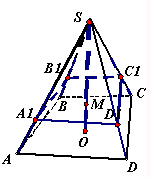 如图,在四棱锥S-ABCD中,SO⊥平面ABCD,O为垂足,点M在SO上,且SM:MO=2:1,经过点M作与底面ABCD平行的平面α,分别交棱SA、SB、SC、SD于A1、B1、C1、D1
如图,在四棱锥S-ABCD中,SO⊥平面ABCD,O为垂足,点M在SO上,且SM:MO=2:1,经过点M作与底面ABCD平行的平面α,分别交棱SA、SB、SC、SD于A1、B1、C1、D1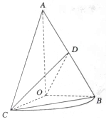 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=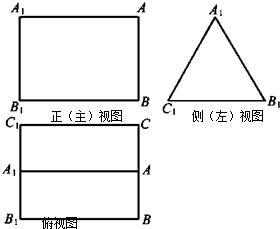 如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.
如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.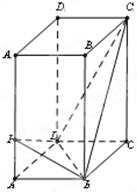 如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.
如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.