题目内容
 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=| 2 |
(Ⅰ)求证:PC⊥BD;
(Ⅱ)若PB=BC,求四棱锥P-ABCD的体积.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取O为AD的中点,连接CO,PO,证明BD⊥OC,PO⊥BD,即可证明BD⊥平面POC,从而可得PC⊥BD;
(Ⅱ)若PB=BC,求出OP,即可求四棱锥P-ABCD的体积.
(Ⅱ)若PB=BC,求出OP,即可求四棱锥P-ABCD的体积.
解答:
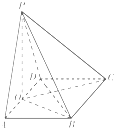 (Ⅰ)证明:取O为AD的中点,连接CO,PO,如图.
(Ⅰ)证明:取O为AD的中点,连接CO,PO,如图.
则在矩形ABCD中,有
=
=
,可得Rt△CDO∽Rt△DAB,
则∠OCD=∠BDA,故∠OCD+∠CDB=90°,
故BD⊥OC,…(3分)
由PA=PD,O为AD中点,可得PO⊥AD,
又平面PAD⊥平面ABCD.
则PO⊥平面ABCD,则PO⊥BD.
又OC?平面POC,PO?平面POC,则有BD⊥平面POC,
又PC?平面POC,故PC⊥BD.…(6分)
(Ⅱ)解:在矩形ABCD中,连接BO,则OB=OC=
=
=
,
又PB=BC=2,则OP=
=
=1,
则四棱锥P-ABCD的体积VP-ABCD=
S矩形ABCD•OP=
×2×
×1=
.…(12分)
 (Ⅰ)证明:取O为AD的中点,连接CO,PO,如图.
(Ⅰ)证明:取O为AD的中点,连接CO,PO,如图.则在矩形ABCD中,有
| CD |
| DO |
| AD |
| AB |
| 2 |
则∠OCD=∠BDA,故∠OCD+∠CDB=90°,
故BD⊥OC,…(3分)
由PA=PD,O为AD中点,可得PO⊥AD,
又平面PAD⊥平面ABCD.
则PO⊥平面ABCD,则PO⊥BD.
又OC?平面POC,PO?平面POC,则有BD⊥平面POC,
又PC?平面POC,故PC⊥BD.…(6分)
(Ⅱ)解:在矩形ABCD中,连接BO,则OB=OC=
| OD2+CD2 |
12+(
|
| 3 |
又PB=BC=2,则OP=
| PB2-OB2 |
22-(
|
则四棱锥P-ABCD的体积VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
点评:本题考查了线面垂直的判定定理、面面垂直的判断定理和性质定理的综合应用,以及四棱锥的体积公式的应用.

练习册系列答案
相关题目
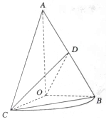 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=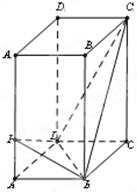 如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.
如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.