题目内容

求f（x）=x2-3ax+a2lnx的单调区间．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导数，通过讨论①当a≤0时②当a＞0时的情况，从而求出函数的单调区间．
解答： 解：由题意得：函数的定义域为x＞0，
f′(x)=2x-3a+
a2
x
=
2x2-3ax+a2
x
=
(2x-a)(x-a)
x
，
①当a≤0时，f′（x）＞0恒成立，
故f（x）在（0，+∞）上递增；
②当a＞0时，令f′（x）＞0⇒x＞a或x＜
a
2
，f′(x)＜0⇒
a
2
＜x＜a
所以f（x）的增区间为(0，
a
2
)，(a，+∞)，减区间为(
a
2
，a)
点评：本题考察了函数的单调性，导数的应用，渗透了分类讨论思想，是一道基础题．
练习册系列答案
相关题目
对空间任意两个向量
a
，
b
（
b
≠0），
a
∥
b
的充要条件是（　　）
A、
a
=
b
B、
a
=-
b
C、
b
=λ
a
D、
a
=λ
b
已知向量
a
=（cos（x+
π
8
），sin2（x+
π
8
）），
b
=（sin（x+
π
8
），1），函数f（x）=2
a
•
b
-1．
（Ⅰ）求函数f（x）的解析式，并写出函数f（x）的周期与对称中心坐标；
（Ⅱ）求函数y=f（-
1
2
x）的单调递增区间．
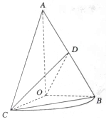如图，已知△AOB，∠AOB=
π
2
，∠BAO=
π
6
，AB=4，D为线段AB的中点．若△AOC是△AOB绕直线AO旋转而成的．记OB绕O旋转所成角∠BOC为θ．
（1）当平面COD⊥平面AOB时，证明：OC⊥OB；
（2）若θ∈[
π
2
，
2π
3
]，求三棱锥C-AOB的体积V的取值范围．
已知数列{an}的前n项和为Sn，且a1=
1
2
，an+1=
n+1
2n
an．
（1）求证：数列{
n
an
}是等比数列；
（2）设bn=n（2-Sn），n∈N*，若集合M={n|bn≥λ，n∈N*}恰有5个元素，求实数λ的取值范围．
已知函数f（x）=
3
sinxcosx+sin2x-
3
2
，将函数f（x）的图象向左平移
π
6
个单位，得到函数g（x）的图象，设△ABC得三个角A，B，C的对边分别是a，b，c
（1）若f（C）=0，c=
6
，2sinA=sinB，求a，b的值；
（2）若g（B）=0，且
m
=（cosA，cosB），
n
=（1，sinA-cosAtanB），求
m
•
n
的取值范围．
为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老人，结果如下：
是否需要志愿者男女
需要5025
不需要200225
（Ⅰ）估计该地区老年人中，需要志愿提供帮助的老年人的比例；
（Ⅱ）能否在犯错误的概率不超过1%的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关？
（Ⅲ）根据（Ⅱ）的结论，能否提出更好的调查办法来估计该地区的老年人中，需要志愿者提供帮助的老年人的比例？说明理由．
设{an}是公差不为零的等差数列，Sn为其前n项和，满足a22+a32=a42+a52，S7=7．
（1）求数列{an}的通项公式；
（2）求数列{an}的前n项和Sn．
观察以下各等式：
sin230°+cos260°+sin30°cos60°=
3
4

sin220°+cos250°+sin20°cos50°=
3
4

sin215°+cos245°+sin15°cos45°=
3
4

分析上述各式的共同特点，猜想出反映一般规律的等式，并对等式的正确性作出证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网