题目内容
已知公比为整数的等比数列{an}中,a1=1,a3=2a2+3,在等差数列{bn}中,公差d=2,且b1+b2+b3=15.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)求数列{an•bn}的前n项和Sn.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)求数列{an•bn}的前n项和Sn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设q为等比数列{an}的公比,依题意,可求得q=3,从而可得数列{an}的通项公式;由等差数列{bn}的公差d=2,且b1+b2+b3=15,可求得{bn}的通项公式;
(Ⅱ)由( I)知Sn=3×1+5×3+7×32+…+(2n-1)×3n-2+(2n+1)×3n-1,3Sn=3×3+5×32+7×33+…+(2n-1)×3n-1+(2n+1)×3n,利用错位相减法即可求得数列{an•bn}的前n项和Sn.
(Ⅱ)由( I)知Sn=3×1+5×3+7×32+…+(2n-1)×3n-2+(2n+1)×3n-1,3Sn=3×3+5×32+7×33+…+(2n-1)×3n-1+(2n+1)×3n,利用错位相减法即可求得数列{an•bn}的前n项和Sn.
解答:
解:( I)设q为等比数列{an}的公比,则由a1=1,a3=2a2+3,
得q2=2q+3,解得q=3或q=-1(舍去).…(2分)
∴{an}的通项公式为an=a1•qn-1=3n-1.…(3分)
∵b1+b2+b3=15,∴b2=5,又d=2,∴b1=b2-d=3.…(5分)
∴bn=3+2(n-1)=2n+1.…(7分)
( II)由( I)知Sn=3×1+5×3+7×32+…+(2n-1)×3n-2+(2n+1)×3n-1①
∴3Sn=3×3+5×32+7×33+…+(2n-1)×3n-1+(2n+1)×3n②
∴①-②得-2Sn=3×1+2×3+2×32+2×33+…+2×3n-1-(2n+1)×3n
=3+2(3+32+33+…+3n-1)-(2n+1)×3n
=3+2×
-(2n+1)×3n
=-2n•3n…(11分)
∴Sn=n•3n.…(12分)
得q2=2q+3,解得q=3或q=-1(舍去).…(2分)
∴{an}的通项公式为an=a1•qn-1=3n-1.…(3分)
∵b1+b2+b3=15,∴b2=5,又d=2,∴b1=b2-d=3.…(5分)
∴bn=3+2(n-1)=2n+1.…(7分)
( II)由( I)知Sn=3×1+5×3+7×32+…+(2n-1)×3n-2+(2n+1)×3n-1①
∴3Sn=3×3+5×32+7×33+…+(2n-1)×3n-1+(2n+1)×3n②
∴①-②得-2Sn=3×1+2×3+2×32+2×33+…+2×3n-1-(2n+1)×3n
=3+2(3+32+33+…+3n-1)-(2n+1)×3n
=3+2×
| 3(1-3n-1) |
| 1-3 |
=-2n•3n…(11分)
∴Sn=n•3n.…(12分)
点评:本题考查等差数列与等比数列的通项公式及其应用,突出考查错位相减法求数列的和,考查等价转化思想与运算能力,属于难题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
设数列{an}的前n项和为Sn,a1=1,an=
+2(n-1),(n∈N*),若S1+
+
+…+
-(n-1)2=2015,则n的值为( )
| Sn |
| n |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
| A、1008 | B、1007 |
| C、2014 | D、2015 |
设双曲线
-
=1上一点P,F1,F2是焦点,若|PF1|=10,则|PF2|等于( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、2 | B、2或18 | C、18 | D、16 |
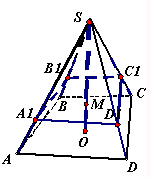 如图,在四棱锥S-ABCD中,SO⊥平面ABCD,O为垂足,点M在SO上,且SM:MO=2:1,经过点M作与底面ABCD平行的平面α,分别交棱SA、SB、SC、SD于A1、B1、C1、D1
如图,在四棱锥S-ABCD中,SO⊥平面ABCD,O为垂足,点M在SO上,且SM:MO=2:1,经过点M作与底面ABCD平行的平面α,分别交棱SA、SB、SC、SD于A1、B1、C1、D1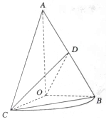 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=