题目内容
(1)已知不等式x2+bx+c>0的解集是{x|x<-1或x>2},求b,c的值;
(2)若x<-1,则x为何值时y=
有最大值,最大值为多少?
(2)若x<-1,则x为何值时y=
| x2+x+1 |
| x+1 |
考点:一元二次不等式的解法,基本不等式
专题:函数的性质及应用,不等式的解法及应用
分析:(1)根据题意,结合根与系数的关系,求出b、c的值;
(2)化简y的解析式,利用基本不等式,求出y的最大值ymax.
(2)化简y的解析式,利用基本不等式,求出y的最大值ymax.
解答:
解:(1)根据题意,方程x2+bx+c=0的两根是-1和2;
由根与系数的关系,得
,
解得b=-1,c=-2;
(2)∵y=
=
=(x+1)+
-1,
当x<-1时,x+1<0,∴-(x+1)>0,
∴-(x+1)+
≥2,∴(x+1)+
≤-2,
当且仅当x=-2时,“=”成立;
∴当x=-2时,y取得最大值ymax=-2-1=-3.
由根与系数的关系,得
|
解得b=-1,c=-2;
(2)∵y=
| x2+x+1 |
| x+1 |
| (x+1)2-x-1+1 |
| x+1 |
| 1 |
| x+1 |
当x<-1时,x+1<0,∴-(x+1)>0,
∴-(x+1)+
| 1 |
| -(x+1) |
| 1 |
| x+1 |
当且仅当x=-2时,“=”成立;
∴当x=-2时,y取得最大值ymax=-2-1=-3.
点评:本题考查了一元二次不等式与对应方程的关系以及基本不等式的应用问题,解题时应结合根与系数的关系,利用转化思想,进行解答,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设双曲线
-
=1上一点P,F1,F2是焦点,若|PF1|=10,则|PF2|等于( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、2 | B、2或18 | C、18 | D、16 |
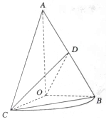 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=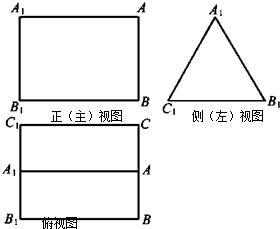 如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.
如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.